TEORIAS E FILOSOFIAS DE GRACELI 151
- Gerar link
- X
- Outros aplicativos
mecânica termodinâmica de vibrações e pressões Graceli no seu sistema decad. e categorial
segunda-feira, 4 de fevereiro de 2019

ou


x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

ou

x
![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

ou

x

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

ou

x

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

ou

x

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Uma função de estado é uma função que descreve uma relação entre duas ou mais variáveis de estado que definem o estado de um sistema termodinâmico. Designa também qualquer variável de estado assumida dependente daquelas escolhidas para definirem-se os estados do sistema e por tal tratadas como independentes.
Definição[editar | editar código-fonte]
Em termodinâmica, as variáveis de estado ou variáveis termodinâmicas são as grandezas físicas termodinâmicas utilizadas na definição e descrição do estado de um sistema termodinâmico.
Algumas das variáveis de estado, comuns a todos os sistemas termodinâmicos massivos, incluso os mais simples, são:
massa (m) ; quantidade de matéria (n) ; Pressão (P) ; Temperatura (T) ; Volume (V) ; Energia interna (U) e Entropia (S).
Há ainda outras, não menos importantes, tais como:
Um estado de um sistema é descrito por um conjunto específicos de valores de suas variáveis de estado. A definição de "estado" do sistema - e mesmo das variáveis de estado - assume em princípio o sistema em equilíbrio termodinâmico.
Um dado sistema termodinâmico altera o seu estado de equilíbrio em virtude de alterações nas interações que estabelece com a sua fronteira ou mesmo vizinhança. Ao fazê-lo, o processo desencadeado pode dar-se e usualmente se dá de forma abrupta o suficiente para que não se possa definir estado de equilíbrio durante a transição entre os assumidos estados de equilíbrio inicial e final. Poucos são os casos onde os processos - então nomeados processos quasi-estáticos - dão-se de forma adequada o suficiente para que se possa corretamente descrevê-los via uma sequência de incontáveis transições diferenciais entre estados de equilíbrio imediatamente adjacentes, ou seja, entre estados quasi-idênticos, de forma que o sistema possa sempre ser assumido estar em equilíbrio termodinâmico em qualquer instante durante a transição.
O conjunto de valores das variáveis de estado define o estado do sistema apenas quando esse encontra-se no equilíbrio termodinâmico, e tais variáveis não podem - ao menos sem considerações muito específicas - ser usadas para descrever a evolução temporal do sistema na grande maioria dos processos termodinâmicos onde, durante a transição de um estado de equilíbrio a outro, o sistema não está em equilíbrio (muitas das variáveis de estado não são sequer definidas em tal situação). Tal descrição é corretamente possível apenas nos processos quasi-estáticos.
Independente da forma como se dá o processo que culmina por levar o sistema de um dado estado a outro qualquer, uma vez comparados os valores das variáveis de estado nos diversos estados de equilíbrio possíveis para o sistema (usualmente mas não necessariamente um sistema fechado), verifica-se contudo que, em qualquer estado, há vínculos e restrições de natureza física conectando os diversos valores possíveis das variáveis de estado. Igualmente satisfeitos em qualquer estado do sistema, são tais vínculos que, nos processos termodinâmicos, não permitem que os valores das variáveis de estado se alterem de forma indiscriminada ou mesmo de forma completamente independente das demais, mesmo que o processo entre os estados seja em essência um processo caótico e de não equilíbrio.
As relações de dependência entre as variáveis - as funções de estado, traduzidas matematicamente na forma de equações de estado - são relações que conectam os possíveis valores de um dado subconjunto de variáveis de estado de um sistema. Dá-se também o nome de "função de estado" às variáveis de estado que são assumidas dependentes de outras - geralmente daquelas escolhidas para definir-se o estado. Assim, a energia interna U de um gás ideal é dita ser uma "função de estado; sendo as variáveis independentes - as que definem o estado no estudo de tais gases - usualmente escolhidas como sendo a temperatura T, a pressão P e o volume V do gás.
É nesses termos e com base no antes exposto que se diz: A variação de uma função de estado depende apenas do estado final e do estado inicial do sistema.
Uma função de estado estabelece relações entre um determinado número de variáveis de estado, mas não necessariamente entre todas simultaneamente, havendo assim várias equações de estado possíveis para um sistema. Uma função de estado usualmente não encerra em si todas as propriedades físicas do sistema, e não é assim capaz, ao menos sozinha, de descrevê-lo completamente. Precisa-se usualmente de um conjunto mínimo de equações de estado independentes para fazê-lo.
É possível contudo escrever-se uma única equação - nomeada equação fundamental - que encerra em si todas as propriedades físicas do sistema. Essa equação descreve, sozinha, todo o sistema, e dela é possível extrair-se todas as equações de estado desejadas. Para fazê-lo basta utilizar o formalismo termodinâmico associado.
Exemplo - Gás monoatômico ideal[editar | editar código-fonte]
Considere um sistema definido por uma certa massa de gás ideal monoatômico. A análise de tal sistema revela que, para ele, há as seguintes equações de estado:
(relação de Clapeyron)
Nas expressões anteriores, n representa a quantidade de matéria do sistema, em mols, e R é a constante dos gases ideais.
As partículas de um gás monoatômico só possuem movimentos de translação e, como se trata de um gás ideal, não interagem entre si. Assim, classicamente, a energia interna deste gás é dependente apenas da energia cinética das partículas, energia que por sua vez liga-se diretamente ao conceito de temperatura do sistema. Logo, nesse caso, a energia interna é função exclusiva da temperatura. Basta saber-se a temperatura de uma amostra de gás ideal em equilíbrio termodinâmico que pode-se, então, determinar sua energia interna.
A relação para a energia interna do gás em função da temperatura acima define uma função de estado. Observe que a energia interna depende da temperatura contudo independe de como o sistema chegou à essa temperatura. Qualquer que seja o processo a qual se submeta o sistema, provido que esse regresse à mesma inicial temperatura T, ter-se-á uma variação nula de sua energia interna.[1]
Observe contudo que pode-se combinar as duas equações acima para se gerar outra equação de estado, uma que envolva a energia interna, a pressão e o volume:
Para um mesmo valor de temperatura e por conseguinte para uma mesma energia interna, há diversos estados possíveis do sistema, cada qual com uma pressão e um volume diferentes.
Embora possam-se cogitar outras equações de estado, nenhuma delas, sozinha, encerram em si todas as informações físicas acerca do sistema.
Ao contrário, uma equação que vincule a energia interna U do gás ideal à sua entropia S, ao seu número de partículas N e ao seu volume V encerrará em si própria todas as informações físicas pertinentes ao sistema assim definido, e constitui assim uma equação fundamental de tal sistema. A título de curiosidade, a equação fundamental para um sistema composto por N partículas de um gás ideal confinados em um volume V e com energia interna U é, na representação da energia, com  representando a constante de Boltzmann e c uma constante adequadamente escolhida:
representando a constante de Boltzmann e c uma constante adequadamente escolhida:
 representando a constante de Boltzmann e c uma constante adequadamente escolhida:
representando a constante de Boltzmann e c uma constante adequadamente escolhida:Através da transformada de Legendre é possível reescrever-se à equação acima, obtendo-se assim várias outras equações fundamentais, cada qual encerrando sozinha todas as informações físicas acerca do sistema em consideração.
Quanto ao conhecimento da força[editar | editar código-fonte]
Vibração determinística[editar | editar código-fonte]
Ocorre quando o valor ou magnitude da excitação, seja ela força ou movimento, aplicada no sistema é conhecida em qualquer instante de tempo.
Vibração aleatória[editar | editar código-fonte]
É aquela que não pode ser prevista, os seus valores não são conhecidos. Como exemplos podemos citar a velocidade do vento e o movimento do solo durante um terremoto.
Quanto aos diversos elementos[editar | editar código-fonte]
- Vibração linear
Ocorre quando todos os componentes básicos do sistema (massa, mola e amortecedor) se comportam de maneira linear, o que não ocorre com a mola depois de uma certa deformação, e portanto passa a possuir um comportamento não linear.
- Vibração não linear
Quando qualquer elemento se comporta de maneira não linear no sistema, temos a vibração não linear, e portanto teremos que lidar com equações diferenciais mais complexas de se resolver e de análises melhor desenvolvidas, cujo principio da superposição não é válido como para o caso de vibrações do tipo linear. Todo sistema tende a comportar-se não linearmente com o aumento da amplitude, como no caso da mola já mencionado.
Forças de excitação[editar | editar código-fonte]
Um sistema mecânico ou estrutural sofre vibração forçada sempre que energia externa é fornecida ao sistema durante a vibração. A energia externa pode ser fornecida ao sistema por meio de uma força aplicada ou por uma excitação de deslocamento imposta. A natureza da força aplicada ou da excitação de deslocamento pode ser da natureza harmônica, não harmônica mas periódica, não periódica ou aleatória. A resposta de um sistema à excitação harmônica é denominada resposta harmônica. A excitação não-periódica pode ser de curta ou longa duração. A resposta de um sistema dinâmico a excitações não-periódicas aplicadas repentinamente é denominada resposta transitória. [1]
Força harmônica[editar | editar código-fonte]
A vibração produzida por uma máquina rotativa desbalanceada, as oscilações de uma chaminé alta provocadas por emissão de vórtices (redemoinhos) sob vento constante e o movimento vertical de um automóvel sobre a superfície senoidal de uma estrada são exemplos de vibração excitada harmonicamente.
 Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou
Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou  ou
ou  . Onde
. Onde  é a amplitude,
é a amplitude,  é a frequência e
é a frequência e  é o ângulo de fase da excitação harmônica. O valor de
é o ângulo de fase da excitação harmônica. O valor de  depende do valor de
depende do valor de  em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]
em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]- Força harmônica pelo desbalanceamento rotativo[1]
Massas desbalanceadas em máquinas rotativas são grandes causadoras de vibração em vários casos de engenharia, como exemplo mais clássico as rodas de um carro que quando estão desbalanceadas causam trepidações no veículo. Um sistema é dito desbalanceado quando o centro de massa desse sistema não coincide com seu centro de rotação. Uma representação simplificada dessa situação pode ser visualizada na figura ao lado. A máquina possui massa  e há uma outra massa
e há uma outra massa  desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez
desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez  e a um amortecedor viscoso de constante de amortecimento
e a um amortecedor viscoso de constante de amortecimento  . Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga
. Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga  . Essa força pode ser decomposta em componentes horizontal
. Essa força pode ser decomposta em componentes horizontal  que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical
que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical  que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular
que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular  . Sendo
. Sendo  a amplitude da vibração,
a amplitude da vibração,  a frequência de oscilação da massa desbalanceada e
a frequência de oscilação da massa desbalanceada e  o ângulo de fase. Os valores de
o ângulo de fase. Os valores de  e
e  são
são
 e há uma outra massa
e há uma outra massa  desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez
desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez  e a um amortecedor viscoso de constante de amortecimento
e a um amortecedor viscoso de constante de amortecimento  . Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga
. Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga  . Essa força pode ser decomposta em componentes horizontal
. Essa força pode ser decomposta em componentes horizontal  que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical
que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical  que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular
que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular  . Sendo
. Sendo  a amplitude da vibração,
a amplitude da vibração,  a frequência de oscilação da massa desbalanceada e
a frequência de oscilação da massa desbalanceada e  o ângulo de fase. Os valores de
o ângulo de fase. Os valores de  e
e  são
são![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)

Equação de movimento[editar | editar código-fonte]
Se uma força  agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:
agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:  . Visto que essa equação é não-homogênea, sua solução geral
. Visto que essa equação é não-homogênea, sua solução geral  é dada pela soma da solução homogênea
é dada pela soma da solução homogênea  com a solução particular
com a solução particular  . A solução homogênea, que é a solução da equação homogênea
. A solução homogênea, que é a solução da equação homogênea  representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular
representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular  , que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
, que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
 agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:
agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:  . Visto que essa equação é não-homogênea, sua solução geral
. Visto que essa equação é não-homogênea, sua solução geral  é dada pela soma da solução homogênea
é dada pela soma da solução homogênea  com a solução particular
com a solução particular  . A solução homogênea, que é a solução da equação homogênea
. A solução homogênea, que é a solução da equação homogênea  representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular
representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular  , que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
, que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]Podemos perceber que  desaparece e
desaparece e  torna-se
torna-se  após algum tempo (
após algum tempo ( na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema
na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema  ,
,  e
e  .
.
 desaparece e
desaparece e  torna-se
torna-se  após algum tempo (
após algum tempo ( na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema
na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema  ,
,  e
e  .
.Força periódica[editar | editar código-fonte]
Excitação que se repete em certo período, porém com intensidades diferentes. Um exemplo prático são motores de combustão interna. Se a força for periódica, mas não-harmônica, ela pode ser substituída por uma soma de funções harmônicas por da expansão da série de Fourier. Usando o princípio da superposição, a resposta do sistema pode ser determinada pela superposição das respostas às funções forçantes harmônicas individuais.[1]
De acordo com a teoria desenvolvida pelo matemático e físico francês Jean Baptiste Joseph Fourier, qualquer função periódica F(t), com período T, pode ser representada por uma série infinita da forma abaixo:

onde  e onde os coeficientes
e onde os coeficientes  ,
,  , e
, e  são dados pelos cálculos a seguir
são dados pelos cálculos a seguir
 e onde os coeficientes
e onde os coeficientes  ,
,  , e
, e  são dados pelos cálculos a seguir
são dados pelos cálculos a seguir


Os coeficientes  ,
,  e
e  , são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
, são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
 ,
,  e
e  , são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
, são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
Força transitória[editar | editar código-fonte]
Excitação caracterizada por uma liberação de energia grande em um intervalo curto de tempo. Inúmeros exemplos descrevem este tipo de força: explosão, impacto, etc
Força aleatória[editar | editar código-fonte]
São forças de excitação que não descrevem um padrão determinístico que possa ser definido por uma equação. Para tratar sistemas excitados por forças aleatórias é necessário utilizar métodos estatísticos. Fenômenos aeroelásticos são exemplos de sistemas excitados por forças aleatórias, como forças em asas de aviões, ventos em colunas de pontes, etc.
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
ou
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD - xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
ou- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD - xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Pressão (símbolo  ) é a relação entre uma determinada força e sua área de distribuição.
) é a relação entre uma determinada força e sua área de distribuição.
 ) é a relação entre uma determinada força e sua área de distribuição.
) é a relação entre uma determinada força e sua área de distribuição.O termo pressão é utilizado em diversas áreas da ciência como uma grandeza escalar que mensura a ação de uma ou mais forças sobre um determinado espaço, podendo este ser líquido, gasoso ou mesmo sólido. A pressão é uma propriedade intrínseca a qualquer sistema, e pode ser favorável ou desfavorável para o homem: a pressão que um gás ou vapor exerce sobre a pá de uma hélice, por exemplo, pode ser convertida em trabalho. Por outro lado, a pressão da água nas profundezas do oceano é um dos grandes desafios para os pesquisadores que buscam novas fontes de recursos naturais.[1]
Expressões matemáticas[]
Para problemas que envolvem gases e sólidos a expressão matemática utilizada para expressar pressão é dada por:
ou
Onde:
é a pressão;
é a força normal a superfície;
é a área total onde a força é aplicada.
Para líquidos, a pressão pode ser escrita como:
ou
Onde:
é a pressão em um ponto específico ou a diferença entre a pressão inicial e final do sistema;
é a massa específica do líquido. ;
é a aceleração gravitacional;
é a profundidade do ponto dentro do líquido.
Podemos descobrir a pressão de um gás a determinada temperatura e volume através da equação do gás ideal:
Onde:
é a pressão do gás;
é o número de mols do gás;
é a constante dos gases perfeitos;
é o volume do gás.
A pressão é uma grandeza escalar. O vetor força muda conforme a orientação do plano onde é aplicado, porém o valor da pressão permanece o mesmo, ou seja, é independente de direção. O vetor força que caracteriza a pressão pode ser relacionado ao vetor da força normal, uma vez que ambos são perpendiculares à superfície. [1]
Unidades[editar | editar código-fonte]
Sendo a definição de pressão: força por unidade de área, analogamente a unidade será newton por metro quadrado (N/m2). Em homenagem a Blaise Pascal, por suas diversas contribuições relativas à pressão, pressão mecânica e hidrostática, a unidade no Sistema Internacional para medir pressão é o Pascal (Pa).
Em geral, a unidade é encontrada na forma de milhar(kPa), uma vez que as medidas de pressão geralmente apresentam valores altos dessa unidade. A pressão exercida pela atmosfera ao nível do mar, por exemplo, corresponde a aproximadamente 101.325 Pa (pressão normal), e esse valor é normalmente associado a uma unidade chamada atmosfera padrão(atm).
Outras unidades[editar | editar código-fonte]
- Atmosfera é a pressão correspondente a 0,760m (760mm) de Mercúrio, com densidade de 13,5951 g/cm³ a uma aceleração gravitacional de 9,80665 m/s².
- Bária é a unidade de pressão no Sistema CGS de unidades e vale uma dyn/cm².
- Bar é um múltiplo da bária, onde 1 bar = 106 bárias.
- PSI (pound per square inch), libra por polegada quadrada, é a unidade de pressão no sistema inglês/americano, onde 1 psi = 0,07 bar.
- milibar ou hectoPascal é um multiplo do pascal, onde 1 hPa = 100 Pa. Geralmente utilizado na meteorologia.
- mmHG, também chamada de Torricelli, é uma unidade de pressão antiga inventada com o surgimento do barômetro, onde 1 mmHG = 133,332 Pa.
- mH2O é uma unidade relativa a pressão necessária para elevar em um metro o nível de uma coluna de água em um barômetro, sendo 1 mH2O = 9806,65 Pa.
- kgf/cm² representa o peso normal do ar ao nível do mar por cm², sendo 1 kgf/cm² = 98066,52 Pa.
| Nomenclatura | Atmosfera | Pascal | Bária | Bar | milibar ou hectopascal | mmHg | mH2O | kgf/cm² |
|---|---|---|---|---|---|---|---|---|
| Unidade | Atm | Pa | Ba | Bar | mBar / hPa | mmHg | mH2O | kgf/cm² |
| Atmosfera | 1,01325×105 | 1,01325×106 | 1,01325 | 1013,25 | 760,0 | 10,33 | 1,033 | |
| Pascal | 9,869×10-6 | 10 | 10-5 | 0,01 | 7,501×10-3 | 1,020×10-4 | 1,019×10-5 | |
| Bária | 9,869×10-7 | 0,1 | 10-6 | 0,001 | 7,501×10-4 | 1,020×10-5 | 1,020×10-2 | |
| Bar | 0,9869 | 100000 | 1000000 | 1000 | 750,1 | 10,20 | 1,020 | |
| mBar ou hPa | 9,869×10-4 | 100 | 1000 | 0,001 | 0,7501 | 1,020×10-2 | 10,20 | |
| mmHg | 1,316×10-3 | 133,3 | 1333 | 1,333×10-3 | 1,333 | 1,360×10-2 | 13,60 | |
| mH2O | 9,678×10-2 | 9807 | 9,807×104 | 9,807×10-2 | 98,06 | 73,56 | 0,100 | |
| kgf/cm² | 0,968 | 9,810×104 | 9,810×105 | 0,9810 | 981,0 | 735,8 | 10,00 |
Instrumentos de medição[editar | editar código-fonte]
Manômetro[editar | editar código-fonte]
O manômetro é um instrumento utilizado para medir a pressão de um líquido ou de um gás.
A experiência pode ser feita de várias maneiras, inclusive o arranjo dos equipamentos pode variar. A técnica para medir a pressão de um fluido consiste em manter o líquido(geralmente mercúrio, devido a sua alta densidade) dentro de um recipiente com duas extremidades que permitam manejar a pressão na entrada e a sua abertura ou fechamento. Nessas extremidades podemos colocar gases ou outros líquidos, dependendo da experiência em questão. De acordo com a altura da coluna de líquido, pode-se estimar a pressão que ela exerce sobre a pressão de entrada (geralmente é a pressão atmosférica) utilizando a equação que relaciona altura e densidade do líquido à pressão que ele exerce no meio.
Outro tipo de manômetro mais sofisticado consiste em um tubo flexível com uma extremidade ligada a um ponteiro e a outra aberta para a passagem de determinado gás ou líquido. Conforme o recipiente enche, a pressão no tubo deforma a geometria do recipiente, que por sua vez acaba deslocando o ponteiro. Esse tipo de manômetro tem um caráter mais prático, e o outro mais didático.[3]
Piezômetro[editar | editar código-fonte]
O piezômetro é um aparelho utilizado para medir a pressão que a água (ou sua ausência) exerce na composição do solo. O equipamento consiste em um tubo no qual uma extremidade é conectada a um recipiente com algum líquido(geralmente mercúrio, devido a sua alta densidade) e a outra é revestida por algum material poroso, como uma esponja, por exemplo. O tubo é então preenchido com água, e o líquido de medição é separado da água por vácuo ou gás. Quando o solo está seco, a água do tubo é absorvida pela terra e a coluna de líquido de medicação sobe. Quando o solo está muito umido o processo contrário ocorre, enchendo completamente o tubo com água e diminuindo a coluna de líquido.
Com a equação para medir pressão em líquidos podemos calcular a poro-pressão(ou carga piezométrica) do solo. Esse tipo de medida é muito útil, pois permite monitorar a umidade do solo e evitar situações extremas, como deslizamentos devido a erosão do solo.[4]
Barômetro[editar | editar código-fonte]

Barômetro feito com uma coluna de mercúrio.
O barômetro é um equipamento que nos permite calcular algumas grandezas indiretamente através da pressão.
O primeiro barômetro consistia em um tubo com um lado fechado e o outro fixado em algum recipiente, de forma a permitir a passagem de algum fluido desse recipiente para dentro do tubo. Adicionando ao pequeno reservatório algum líquido(geralmente mercúrio, devido a sua alta densidade) para que este sirva como um indicador. Conforme sabemos da hidrostática, um líquido exerce pressão igual para todos os lados. Assim sendo, quando a parte externa do recipiente for submetida a determinada pressão, o líquido vai exercer a mesma pressão na parte interna do tubo. Caso essa pressão externa seja maior que a interna, a coluna do líquida vai subir a fim de nivelar o sistema. Caso contrário, a coluna desce e a parte de cima fica com vácuo.
Partindo da equação que relaciona a diferença de altura do líquido com a sua pressão, e sabendo qual a pressão interna do tubo, podemos calcular quanto vale a pressão externa em qualquer lugar. Através dessa experiência (conhecida como experiência de Torricelli) podemos determinar a altura do local onde estamos com relação ao nível do mar. Sabe-se que uma coluna de mercúrio, por exemplo, mede 76cm ao nível do mar, e que esse valor diminui quando alcançamos altitudes maiores, pois a pressão atmosférica é menor.[3]
Pressão em gases[editar | editar código-fonte]
Segundo a teoria cinética dos gases, um gás é composto por um grande número de moléculas que se movimentam muito rápido e de forma aleatoria, causando frequentes colisões entre as moléculas do gás e com as paredes de qualquer tipo de recipiente. Essas moléculas apresentam um certo momento, dado pelo produto entre a massa e a velocidade da molécula. No instante em que uma molécula colide com uma parede, as moléculas transmitem momento à superfície, e como consequencia produzem uma força perpendicular à essa superfície. A soma de todas essas forças oriundas de colisões em uma determinada superfície, dividida pela área da mesma, resulta na pressão exercida por um gás em um determinado recipiente.[1]
Algumas aplicações da pressão nos gases podem ser observadas na utilização da pressão que o vapor da água exerce sobre determinada superfície quando confinado em um espaço fechado. Esse processo pode ser encontrado em usinas nucleares, onde uma pá gira com a pressão do vapor e converte essa energia em eletricidade. Além disso, observamos a pressão em gases sendo utilizada diariamente no freio do ônibus, por exemplo. O freio de veículos pesados conta com um sistema que usa ar comprimido para cessar o movimento.
Pressão em fluidos[editar | editar código-fonte]
Um corpo no estado líquido é caracterizado por apresentar uma distância entre suas moléculas que permite ao corpo adequar-se ao ambiente em que se encontra. As características da pressão nos líquidos é semelhante a que encontramos nos gases: o líquido exerce pressão para todos os lados de um recipiente e em qualquer corpo que for imerso nele.
Segundo o princípio de Pascal, ao exercermos pressão em um fluido confinado em um recipiente, essa é transmitida integralmente a todos os ponto desse recipiente. Uma experiências que pode ajudar a compreender esse princípio é a dos vasos comunicantes: Ao armazenarmos algum líquido em uma estrutura com colunas de volumes diferentes podemos observar que o líquido preenche todas as colunas a mesma altura, desconsiderando as diferenças de volume. Isso prova que o fluido espalha-se uniformemente, portanto, exerce pressão igual em todas as direções.[1] Essa demonstração foi muito importante para o surgimento dos sistemas hidraulicos, essenciais nos dias de hoje.
A pressão em líquidos tem algumas diferenças da pressão nos gases. Com os gases, quanto maior a altitude menor a pressão, já com os líquidos, quanto maior a profundidade, maior a pressão. Isso é facil de ser evidenciado - basta mergulhar e automaticamente sentimos a pressão aumentando. É instintivo pensar que ao furar uma garrafa de água, a vazão de um furo na sua base será maior do que a de um furo lateral(considerando que ambos tem a mesma área). Essa diferença é devida a maior pressão no fundo da garrafa, devido a altura da coluna de água.[3]
Outra característica marcante da pressão nos líquidos e demais estados da matéria é sua propriedade de alterar os outros elementos do conjunto: temperatura, pressão e volume. Podemos perceber isso ao cozinhar feijão em uma panela de pressão: o vapor da água aumenta a pressão no interior da panela, e isso provoca uma alteração do ponto de ebulição da água, que passa a ferver acima dos 100°C. Isso agiliza o processo de cozimento do grão do feijão, que seria muito mais lento se não fosse o advento da panela de pressão.
Pressão em sólidos[editar | editar código-fonte]
Existe uma área da física que aborda o assunto pressão com restrição aos corpos rígidos. Esse assunto é estudado profundamente devido as sua extrema importância. A tensão mecânica, como é chamada, estuda todos os tipos de pressões e tensões que são encontradas dentro ou sobre um corpo material, sendo elas:
- Tensão de tração;
- Tensão de compressão;
- Tensão de cisalhamento;
- Tensão elástica;
- Tensão plástica;
- Tensão de escoamento.[5]
Diferente da pressão nos fluidos, em corpos rígidos os átomos não têm tanta liberdade e acabam tendo seus movimentos restringidos, ou seja, não exercem pressão ao seu redor. Se pegarmos uma pedra e largarmos em uma superfície, a única pressão que a pedra exerce no sistema é a resultante de sua força peso e da área da sua base, que pressiona a mesa. Portanto, percebemos que a pressão dos sólidos é ocasionada necessariamente por uma força(a própria força peso, por exemplo) que usa o sólido como recurso para ampliar sua força e área. Este conjunto de informações é suficiente para refletir sobre as consequências dessas tensões no ambiente em que vivemos.
Uma aplicação para essas observações são os patins. A patinação sobre o gelo utiliza dos artifícios da pressão para proporcionar menos aderência aos praticantes do esporte. Vamos entender por quê:
O metal utilizado como lâmina na sola do sapato de patinação é muito fino, e sua área é muito pequena frente ao peso do patinador. Como a pressão é inversamente proporcional a área de abrangência da força, quanto menor o metal mais pressão será feita sobre o gelo.
Assim como a água, o gelo sofre algumas mudanças de características. A que estamos interessados no momento revela que o gelo sobre os patins está sobre uma pressão tão intensa que acaba trocando de estado da matéria e vira liquido mesmo a temperaturas abaixo de zero. Graças a isso, os patins utilizam a força peso do patinador para derreter uma fina camada de gelo em baixo da lâmina quando está deslizando, aumentando sua velocidade e lubrificando o caminho.[1]
Alguns fenômenos naturais como os glaciares também tem alguns fatores relacionados a pressão que os cubos de gelo exercem um sobre o outro, fazendo com que o gelo mais em baixo derreta e o gelo que está por cima,fazendo uma trilha de água e escoe os blocos até algum rio ou oceano(ou até que sequem).
efeitos Graceli de piezoeletricidade
A piezoeletricidade tem também efeitos proporcionais sobre magnetismo, condutividade térmica e elétrica, dilatações, interações interna e transformações de estruturas, difrações e refrações, emissões e absorções de partículas e energias, momentum térmico, elétrico, dinãmico, magnético, e outros fenômenos. ondas e saltos quântico, estado quântico de partículas, momentum quântico.
A piezoeletricidade tem também efeitos proporcionais sobre magnetismo, condutividade térmica e elétrica, dilatações, interações interna e transformações de estruturas, difrações e refrações, emissões e absorções de partículas e energias, momentum térmico, elétrico, dinãmico, magnético, e outros fenômenos. ondas e saltos quântico, estado quântico de partículas, momentum quântico.

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.
Mecanismo
O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).
O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.[1]
Cristais[editar | editar código-fonte]
Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.
Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.
Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.
A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.[2]
Descrição matemática[editar | editar código-fonte]
A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:[3]

Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinalaplicada.
Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.
Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:

Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.
A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que  e
e  . Assim, temos
. Assim, temos
 e
e  . Assim, temos
. Assim, temos

onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.
Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.
Num material piezoelétrico também interessam os seguintes coeficientes:
- Coeficiente de acoplamento eletro-mecânico:
 é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.- Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:

Aplicações[editar | editar código-fonte]
O fenômeno piezoelétrico é encontrado em aplicações úteis, como a produção e detecção de som, a geração de tensões elevadas, geração de frequências eletrônicas, microbalanças e concentração ultrafina de conjuntos ópticos. É também a base de uma série de técnicas científicas instrumentais com resolução atômica (microscopia de varredura de sonda), e os usos cotidianos, como atuando como fonte de ignição para isqueiros de faísca elétrica, microfones, e as famosas "pílulas" ou cápsulas de guitarra (embora sejam utilizadas em guitarras acústicas, baixos, violoncelos e outros), que representam uma espécie de microfone. O projeto mais arrojado; porém, refere-se à utilização do materiais piezoelétricos em ruas e estradas, onde a pressão causada pela movimentação dos carros podem ser usados para gerar eletricidade de forma barata.
As transformações que ocorrem em cada material:
- Exemplos de transformações mecânico-elétrica
- Medidor de pressão;
- Microfone;
- Isqueiro elétrico;
- Alarme antifurto;
- Agulha do toca-discos.
- Exemplos de transformações elétrico-mecânicas
- Ultrassom;
- Nebulizadores;
- Aparelhos elétricos contra mosquitos;
- Alto-falantes;
Sensores piezoelétricos[editar | editar código-fonte]
Os sensores piezoelétricos mensuram determinados parâmetros físicos, que estão na forma de tensão mecânica ou variações de cargas elétricas. Estes são utilizados para se medir pressão cardíaca e registrar os batimentos cardíacos, emitir ou recepcionar ultrassons a fim de visualizar órgãos humanos através da conversão da energia proveniente das ondas emitidas pelo funcionamento dos órgãos que faz vibrar uma lâmina de material piezoelétrico. Resumidamente, quando se aplica tensão mecânica, há o aparecimento de um potencial elétrico; quando a tensão aplicada for de natureza elétrica, temos uma deformação física.
O princípio de funcionamento de um sensor piezoelétrico reside no fato de que dada dimensão física, pela ação de uma força, é deformada. Dependendo da concepção de um sensor, "modos" diferentes de polarização sobre o elemento piezoelétrico podem ser usados (eles podem ser comprimidos transversalmente, longitudinalmente, ou pela ação de cisalhamento).
A detecção de variações de pressão sob a forma de ondas sonoras é a aplicação mais comum do sensor. Por exemplo, Microfonepiezoelétricos, onde ondas sonoras batem no material piezoelétrico, criando uma tensão que varia. Captadores piezoelétricos funcionam pelo mesmo princípio em guitarras electro-acústicas.
Sensores piezoelétricos mais acurados são utilizados com som de alta freqüência (acima de 20000 Hz) em transdutores de ultrassom para imagens médicas. Cada transdutor possui uma freqüência de ressonância natural, tal que quanto menor a espessura do cristal que o compõem, maior será a sua frequência de vibração e melhor será o sinal que este gerará ou será capaz de emitir.
Para várias técnicas de detecção, o sensor pode atuar tanto como um sensor ou então como captador, sendo então preferencialmente chamado transdutor (termo preferido para descrever quando o dispositivo funciona com ambas aplicações). A maioria dos dispositivos piezoelétricos têm esta propriedade de reversibilidade, sendo que desta forma, materiais piezoelétricos são indiscriminadamente chamadas transdutores. Transdutores de ultrassom, por exemplo, pode projetam ondas de ultrassom no corpo humano, recebem a reverberação desta onda, com frequência diferente da emitida, convertendo-a em sinal elétrico (tensão).
A carga induzida  num material piezo é proporcional a força
num material piezo é proporcional a força  aplicada.
aplicada.
 num material piezo é proporcional a força
num material piezo é proporcional a força  aplicada.
aplicada.
onde  é uma constante piezoelétrica, com unidade Coulomb por Newton.
é uma constante piezoelétrica, com unidade Coulomb por Newton.
 é uma constante piezoelétrica, com unidade Coulomb por Newton.
é uma constante piezoelétrica, com unidade Coulomb por Newton.Os materiais piezoelétricos possuem resistência muito elevada, mas não infinita. Se uma deflexão for aplicada sobre o material, uma corrente infinitesimal seguirá por um circuito, preservando o sinal elétrico gerado pelo piezoelétrico, sendo que a voltagem gerada pode ser mensurada ou ativar outro sensor piezoelétrico deste circuito. Deve-se ressaltar que o sinal decai exponencialmente pela resistência do material piezo somado a resistência externa do circuito.[4]
Padrão de frequência[editar | editar código-fonte]
Materiais piezoelétricos são empregados em relógios como osciladores. Um cristal de quartzo, que utiliza uma combinação dos efeitos de piezoeletricidade direta e inversa para gerar uma série regular de impulsos elétricos cronometrado, que marcam o tempo. O cristal de quartzo (como qualquer material elástico) tem uma frequência natural definida com precisão (devido a sua forma e tamanho), e este é utilizado para estabilizar a frequência de uma tensão elétrica periódica aplicada ao cristal.
O mesmo princípio é aplicado em todos os transmissores e receptores de rádio, e em computadores onde ele cria um pulso de clock. Ambos costumam usar multiplicadores de frequência para atingir faixas gigahertz.
Sonar[editar | editar código-fonte]
Pelos estudos de Leonardo DaVinci no século XV, temos uma descrição simplista, porém clara, da ação de um sonar:
Qualquer outra descrição difere somente em detalhes.
O estudo da natureza das ondas sonoras na água e o modo como elas se propagam permitiu com que se construíssem sistemas acústicos para observação e mapeamento de solos embaixo d'água. Sensores capazes de identificar a energia de ondas acústicas embaixo d'água são chamados Hidrofone, feitos a partir de materiais piezoelétricos.
Os sonares funcionam pela propagação de ondas acústicas (criadas através de sinais digitais eletrônicos) sendo que ele também recebe a volta o sinal acústico que emitiu. Construído com materiais piezoelétricos, este utiliza da energia das ondas para fazer vibrar (sonar) uma película fina que converte a energia proveniente das ondas reverberadas novamente em pulsos elétricos, mas agora com outras intensidades, que são então decodificados em um computador, tratadas, e gerar imagens de regiões abaixo d'água.
O método acústico na fabricação de sonares, o qual não envolve transformações eletroacústicas, representa o método mais rudimentar (baseado na descrição de DaVinci), sendo que este foi amplamente utilizado durante a Primeira Guerra Mundial. Virtualmente, todos os sistemas de sonares, os quais a energia é restrita a forma acústica são utilizados ainda para localizar um alvo quando este é uma fonte primária de som. Neste caso, capta-se apenas a energia proveniente da propagação destas ondas, para então transformá-las em sinas elétricos (através de materiais piezoelétricos) a serem interpretados.
Sonares eletroacústicos são muito mais utilizados, com uma gama maior de aplicações. Porém, para operar, o sonar eletroacústico deve estar parado, muito próximo do local a ser mapeado. Além disso, para ser interpretado, o som deve estar na faixa audível; quando a energia acústica é convertida em energia elétrica, uma vasta gama de equipamentos deve ser aplicada para criar um sinal com características específicas mais convenientes para que os dados possam ser lidos. Neste momento, transdutores como microfones, alto-falantes e fones-de-ouvido (que são excelentes sistemas quando utilizados com deslocamento de massas de ar) se mostram ineficientes com a energia das camadas de água, uma vez que a impedância acústica específica da água (magnitude da resposta a um estímulo) é 4000 vezes maior do que a do ar.
Os sonares eletroacústico são então sistemas muito sensíveis, e desta forma, também são muito suscetíveis a distúrbios e interferências na recepção do sinal. Este tipo de sonar, portanto, ainda é muito estudado e muitos materiais piezoelétricos são testado para que se consiga a melhor relação entre as dificuldades apresentadas por mares e oceanos e pela tecnologia empregada.
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.


 = entropia reversível
= entropia reversível
 [1b]
[1b]

 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível

tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Poço de potencial quântico no sistema decadim. e categorial Graceli
sábado, 9 de fevereiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
 [1b]
[1b]x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Em física, a partícula em uma caixa (também conhecida como poço de potencial infinito) é um problema muito simples que consiste de uma só partícula que rebate-se dentro de uma caixa imóvel da qual não pode escapar, e onde não perde energia ao colidir contra suas paredes.
Em mecânica clássica, a solução ao problema é trivial: a partícula se move em uma línha reta a uma velocidade constante até que rebate em uma das paredes. Ao rebater, a velocidade é alterada apenas na componente perpendicular à parede, que troca de sinal; o módulo da velocidade não se altera. Uma das soluções possíveis é uma partícula absolutamente estacionária, ou seja, com velocidade zero.
O problema se torna muito interessante quando se tenta resolver dentro da mecânica quântica, já que é necessário introduzir muitos dos conceitos importantes desta disciplina para encontrar uma solução. Entretanto, ainda assim é um problema simples com uma solução definida. Este artígo se concentra na solução dentro da mecânica quântica.
Descrição quântica do problema
O problema pode apresentar-se em qualquer número de dimensões, mas o mais simples é o problema unidimensional, ainda que o mais útil é o que se centra em uma caixa tridimensional. Em uma dimensão, se representa por uma partícula que existe em um segmento de uma linha, sendo as paredes os pontos finais do segmento.
Em termos da física, a partícula em uma caixa se define como uma partícula pontual, encerrada em uma caixa onde não experimenta nenhum tipo de força (ou seja, sua energia potencial é constante, ainda que sem perda de generalidade podemos considerar que vale zero). Nas paredes da caixa, o potencial aumenta até um valor infinito, fazendo-a impenetrável. Usando esta descrição em termos de potenciais nos permite usar a equação de Schrödinger para determinar uma solução.
Como se menciona acima, se estivéssemos estudando o problema sob as regras da mecânica clássica, deveríamos aplicar as leis do movimento de Newton às condições iniciais, e o resultado seria razoável e intuitivo. Em mecânica quântica, quando se aplica a equação de Schrödinger, os resultados não são intuitivos. Em primeiro lugar, a partícula só pode ter certos níveis de energia específicos, e o nível zero não é um deles. Em segundo lugar, as probabilidades de detectar a partícula dentro da caixa em cada nível específico de energia não são uniformes - existem várias posições dentro da caixa onde a partícula pode ser encontrada, mas também há posições onde é impossível fazê-lo. Ambos resultados diferem da maneira usual na que percebemos o mundo, inclusive se estão fundamentados por princípios extensivamente verificados através de experimentos.
Caixa monodimensional[editar | editar código-fonte]
A versão mais precisa se dá na situação idealizada de uma "caixa monodimensional", na que a partícula de massa m pode ocupar qualquer posição no intervalo [0,L]. Para encontrar os possíveis estados estacionários é necessário aplicar a equação de Schrödinger independente do tempo em uma dimensão para o problema:
[1]
Considerando que o potencial é zero dentro da caixa e infinito fora, e observando que a função de onde se anula fora da caixa, temos as seguintes condições de contorno:
[1a]
e onde
é a Constante reduzida de Planck,
é a massa da partícula,
é a função de onda estacionária independente do tempo[1] que queremos obter (funções próprias) e
é a energia da partícula (valor próprio).
As funções próprias e valores próprios de uma partícula de massa m em uma caixa monodimensional de comprimento L são:
[1b]
Note-se que só são possíveis os níveis de energia "quantizados". Além disso, como n não pode ser zero (ver mais adiante), o menor valor da energia tampouco pode sê-lo. Esta energia mínima se chama energia do ponto zero e se justifica em termos do princípio de incerteza. Devido a que a partícula se encontra restringida a mover-se em uma região finita, a variância da posição tem um limite superior (o comprimento da caixa,  ). Assim, de acordo com o princípio de incerteza, a variância do momento da partícula não pode ser zero e, portanto, a partícula deve ter uma certa quantidade de energia que aumenta quando a longitude da caixa L diminui.
). Assim, de acordo com o princípio de incerteza, a variância do momento da partícula não pode ser zero e, portanto, a partícula deve ter uma certa quantidade de energia que aumenta quando a longitude da caixa L diminui.
 ). Assim, de acordo com o princípio de incerteza, a variância do momento da partícula não pode ser zero e, portanto, a partícula deve ter uma certa quantidade de energia que aumenta quando a longitude da caixa L diminui.
). Assim, de acordo com o princípio de incerteza, a variância do momento da partícula não pode ser zero e, portanto, a partícula deve ter uma certa quantidade de energia que aumenta quando a longitude da caixa L diminui.
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
EstadologiO poço de potencial representa a energia potencial em forma de poço envolvida num certo sistema e pode ser qualificado como finito ou infinito. Um poço de potencial é a região em torno de um mínimo local de energia potencial que, por sua vez, é a forma de energia que está associada a um certo sistema, no qual ocorre interações entre diferentes corpos, e está relacionada com a posição que determinado corpo ocupa.
A energia potencial de um sistema pode ter quatro origens distintas que estão correlacionadas as quatro forças fundamentais da natureza: força eletromagnética, força gravitacional, força fraca e força forte.
Sob uma perspectiva quântica, o poço de potencial representa o confinamento quântico da partícula em questão e pode provocar a quantização da energia da mesma, o que, classicamente, não acontece.
Visão geral
A energia pode ser liberada a partir de um poço de potencial, se energia suficiente for adicionada ao sistema de tal modo que o máximo local seja superado. Em física quântica, uma partícula pode ser capaz de superar uma barreira de potencial com energia superior à energia da partícula devido devido às características probabilísticas advindas da função de onda das partículas quânticas. Nestes casos, a partícula pode tunelar através das paredes de um poço de potencial.
A partir de uma analogia clássica, pode-se pensar no gráfico de uma função energia potencial bidimensional como sendo uma superfície de energia potencial, que pode ser imaginada de forma semelhante à superfície da Terra em uma paisagem de colinas e vales. Sendo assim, um poço de potencial seria análogo a um vale rodeado por todos os lados por terrenos mais altos e que, portanto, pode ser preenchido com água (por exemplo, ser um lago) sem qualquer água fluindo para um outro mínimo mais baixo (por exemplo, o nível do mar). No caso da gravidade, a região em torno de uma massa é um poço de potencial gravitacional, a menos que a densidade de massa seja tão pequena que as forças de maré de outras massas sejam maiores do que a gravidade do próprio corpo. Uma colina de potencial é o oposto de um poço de potencial, e é a região em torno de um máximo local.
Confinamento quântico[editar | editar código-fonte]
O confinamento quântico pode ser observado quando o diâmetro de confinamento do sistema for da mesma ordem de magnitude do comprimento de onda de de Broglie da partícula confinada. O potencial confinador pode ter origem em barreiras de potenciais devidos a interfaces entre estruturas ou em campos aplicados ao sistema. As propriedades eletrônicase ópticas do material são significativamente afetadas quando suas dimensões são drasticamente alteradas. Isso se deve basicamente por serem mais pronunciados os efeitos causados pelo confinamento em certa direção do material, dentre eles pode-se perceber que existe uma quantização da energia que as partículas podem assumir.
É interessante notar que a solução formal da equação de Schrödinger para sistemas confinados dá ênfase à relação entre a energia e a evolução temporal da fase da função de onda da partícula. A função de onda da partícula é uma função de onda coerente, i.e. a fase da onda só pode mudar por efeito da evolução temporal e por ação determinística de forças. Os efeitos quânticos são preservados quando a função de onda se comporta de maneira coerente. Em sólidos reais, os elétrons geralmente experimentam espalhamentos aleatórios tanto de forma elástica quanto inelástica, a menos que se faça controle preciso das condições e mantenha-se a coerência da função de onda da partícula.
Sistemas de baixa dimensionalidade[editar | editar código-fonte]
O confinamento quântico introduz o estudo de estruturas nas quais as dimensões da amostra e/ou a existência de interfaces entre materiais distintos afloram novas propriedades, inclusive alterações na dimensão espacial efetiva do sistema. Nesse aspecto, a física de sistemas de baixa dimensionalidade usa dos conceitos advindos da mecânica quântica para explorar as propriedades de sistemas confinados e suas possíveis aplicabilidades.[1]
Poços quânticos[editar | editar código-fonte]
No contexto de sistemas nanoestruturados, são denominados genericamente poços quânticos os sistemas estruturados em camadas, que são homogêneos e macroscópicos em duas dimensões, mas apresentam interfaces entre as camadas ao longo da direção perpendicular, sendo essas camadas suficientes para causar confinamento quântico, definindo, assim, um poço nessa direção.
De forma geral, tem-se um sistema tridimensional com um potencial que varia apenas ao longo de uma das direções. Através da solução da equação de Schrödinger percebe-se que as energias resultantes descrevem uma partícula livre em duas dimensões enquanto que confinada, e, portanto, com energias quantizadas, em uma direção. Isso configura um gás de elétrons bidimensional.[1]
Fios quânticos[editar | editar código-fonte]
É possível construir heteroestruturas nas quais o confinamento quântico se dá em duas direções e mantendo uma das direções livre. Isto caracteriza um fio quântico. Nele, percebe-se, através da solução da equação de Schrödinger para o sistema, que em duas direções existirão energias quantizadas enquanto que na outra tem-se um gás de elétrons unidimensional. Através de uma análise menos superficial, nota-se que densidade de estados no nível de Fermi é importante na determinação das quantidades termodinâmicas e coeficientes de transporte do material e que o confinamento quântico tem efeito marcante sobre a forma relevante da densidade de estados. Considerando o exposto, podemos inferir mudanças nas propriedades de transporte eletrônico de sistemas confinados e pode-se perceber que as características de um fio quântico diferem substancialmente de fios metálicos macroscópicos. A condutância de um fio quântico depende apenas de constantes universais e não de características extensivas do sistema, tais como geometria e material.

Onde M é o número de canais definidos pelo par de números quânticos associados à quantização devida ao confinamento em direções transversais. A condutância quântica é completamente independente tanto da geometria quanto do material e é relacionado basicamente com constantes universais.[1]
Pontos quânticos[editar | editar código-fonte]
O último passo na sequência é também confinar a terceira dimensão, o que caracteriza um ponto quântico. Neste caso, não resta nenhuma dimensão livre e configura uma nanopartícula.[1]a Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Gás de Bose no sistema decad. e categorial Graceli
quinta-feira, 14 de fevereiro de 2019
Um gás de Bose ideal é uma versão quântica de um gás ideal clássico. Ele é composto de bósons, partículas que têm um valor inteiro de spin, e portanto obedecem a estatística de Bose-Einstein. A mecânica estatística de bósons foi desenvolvida por Satyendra Nath Bose para fótons, e estendida posteriormente por Albert Einstein para partículas massivas. Einstein percebeu que um gás ideal de bósons iria se condensar quando a temperatura fosse baixa o suficiente, o que não ocorre com um gás ideal clássico. Esta fase da matéria ficou conhecida como Condensado de Bose-Einstein.
Potencial termodinâmico[editar | editar código-fonte]
Devido a Interação de troca, a maneira mais simples de trabalhar com gases quânticos é com o ensemble grande canônico:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
que para um gás fica:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
A segunda soma é restrita ao número total de partículas ser  . Uma maneira de fazer tal soma é somar primeiro sobre todos os
. Uma maneira de fazer tal soma é somar primeiro sobre todos os  possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de
possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de  é permitido, logo:
é permitido, logo:
 . Uma maneira de fazer tal soma é somar primeiro sobre todos os
. Uma maneira de fazer tal soma é somar primeiro sobre todos os  possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de
possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de  é permitido, logo:
é permitido, logo:- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
O potencial termodinâmico é então:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Se o gás possuir apenas graus de liberdade translacionais em  dimensões (os demais casos podem ser tratados de forma análoga):
dimensões (os demais casos podem ser tratados de forma análoga):
 dimensões (os demais casos podem ser tratados de forma análoga):
dimensões (os demais casos podem ser tratados de forma análoga):- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Note que a função polilogarítmica só está definida para  reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
 reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.Condensação de Bose-Einstein[editar | editar código-fonte]
O gás de bósons é o sistema mais simples que apresenta o fenômeno de condensação de Bose-Einstein. Para ver esse efeito, escrevemos o número médio de partículas:
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
O maior valor da função polilogarítmica acontece em  quando o número de partículas em estados excitados é:
quando o número de partículas em estados excitados é:
 quando o número de partículas em estados excitados é:
quando o número de partículas em estados excitados é:- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Perceba que para  isso é um número finito que é atingido numa certa temperatura
isso é um número finito que é atingido numa certa temperatura  . Todas as demais
. Todas as demais
 isso é um número finito que é atingido numa certa temperatura
isso é um número finito que é atingido numa certa temperatura  . Todas as demais
. Todas as demais- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
partículas deverão estar no estado fundamental, não importando quantas sejam (contanto que a aproximação de gás continue valendo).
Um gás de Bose ideal é uma versão quântica de um gás ideal clássico. Ele é composto de bósons, partículas que têm um valor inteiro de spin, e portanto obedecem a estatística de Bose-Einstein. A mecânica estatística de bósons foi desenvolvida por Satyendra Nath Bose para fótons, e estendida posteriormente por Albert Einstein para partículas massivas. Einstein percebeu que um gás ideal de bósons iria se condensar quando a temperatura fosse baixa o suficiente, o que não ocorre com um gás ideal clássico. Esta fase da matéria ficou conhecida como Condensado de Bose-Einstein.
Potencial termodinâmico[editar | editar código-fonte]
Devido a Interação de troca, a maneira mais simples de trabalhar com gases quânticos é com o ensemble grande canônico:
que para um gás fica:
A segunda soma é restrita ao número total de partículas ser  . Uma maneira de fazer tal soma é somar primeiro sobre todos os
. Uma maneira de fazer tal soma é somar primeiro sobre todos os  possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de
possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de  é permitido, logo:
é permitido, logo:
 . Uma maneira de fazer tal soma é somar primeiro sobre todos os
. Uma maneira de fazer tal soma é somar primeiro sobre todos os  possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de
possíveis e depois multiplicar todos os níveis. Para um sistema de bósons, qualquer valor de  é permitido, logo:
é permitido, logo:O potencial termodinâmico é então:
Se o gás possuir apenas graus de liberdade translacionais em  dimensões (os demais casos podem ser tratados de forma análoga):
dimensões (os demais casos podem ser tratados de forma análoga):
 dimensões (os demais casos podem ser tratados de forma análoga):
dimensões (os demais casos podem ser tratados de forma análoga):Note que a função polilogarítmica só está definida para  reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
 reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.
reais menores ou iguais a 1. O segundo termo que já estava presente na expressão anterior é a contribuição de momento zero, ou seja, do estado de menor energia.Condensação de Bose-Einstein[editar | editar código-fonte]
O gás de bósons é o sistema mais simples que apresenta o fenômeno de condensação de Bose-Einstein. Para ver esse efeito, escrevemos o número médio de partículas:
O maior valor da função polilogarítmica acontece em  quando o número de partículas em estados excitados é:
quando o número de partículas em estados excitados é:
 quando o número de partículas em estados excitados é:
quando o número de partículas em estados excitados é:Perceba que para  isso é um número finito que é atingido numa certa temperatura
isso é um número finito que é atingido numa certa temperatura  . Todas as demais
. Todas as demais
 isso é um número finito que é atingido numa certa temperatura
isso é um número finito que é atingido numa certa temperatura  . Todas as demais
. Todas as demaispartículas deverão estar no estado fundamental, não importando quantas sejam (contanto que a aproximação de gás continue valendo).
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível





 = entropia reversível
= entropia reversível
![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)

 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível
 Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou
Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou  ou
ou  . Onde
. Onde  é a amplitude,
é a amplitude,  é a frequência e
é a frequência e  é o ângulo de fase da excitação harmônica. O valor de
é o ângulo de fase da excitação harmônica. O valor de  depende do valor de
depende do valor de  em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]
em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)






 Ver artigo principal: Unidades de pressão
Ver artigo principal: Unidades de pressão

 Ver artigo principal: Hidrostática
Ver artigo principal: Hidrostática


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível




 é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.

"Se você estiver no meio do oceano, e parar seu navio, posicionando um longo tubo em direção ao fundo do mar e colocando a outra extremidade próxima de seu ouvido, você ouvirá navios a grande distância de você."
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Ligação iônica no sistema decadimensional e categorial Graceli
sexta-feira, 8 de fevereiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Ligação iônica (português brasileiro) ou iónica (português europeu) é um tipo de ligação química baseada na atração eletrostática[1] de íons com cargas opostas. Na formação da ligação iônica o metal do elétron, devido a sua baixa eletronegatividade[2] formando um íon positivo ou cátion, ao não metal que acomoda esse elétron na camada de valência tornando-se ânion. No sal de cozinha a ligação química entre os íons sódio e cloreto é iônica. O átomo do não metal tem uma configuração eletrônica semelhante a de um gás nobre, quase totalmente preenchida de elétrons. Ele têm alta eletronegatividade e facilmente ganha um elétron formando um íon negativo ou ânion. A ligação Iônica é a mais forte das ligações primárias.
A ligação iônica ocorre somente se a variação da energia total da reação é favorável—quando os átomos ligados têm energia mais baixa que os átomos livres. Quanto maior a variação da energia total, mais forte se torna a ligação.
Estudos revelaram que não existe ligação iônica pura. Todas ligações iônicas têm um grau de ligação covalente ou ligação metálica. Quanto maior a diferença na eletronegatividade entre dois átomos mais iônica se torna a ligação. Compostos iônicos conduzem eletricidade quando fundidos ou em solução. Eles geralmente têm um alto ponto de fusão e tendem a ser solúveis em água.
Efeitos da polarização

Imagem de dois íons, por exemplo Na+ e Cl- formando uma ligação iônica. Os orbitais eletrônicos geralmente não se sobrepõem (i.e., orbitais moleculares não são formados), devido ao fato de que cada íon chega ao estado energético mais baixo e a ligação é baseada somente (teoricamente) em interações eletrostáticas entre os íons positivo e negativo.
Os íons em cristais de compostos predominantemente iônicos são esféricos, mas, se o íon positivo é pequeno e/ou altamente carregado, será distorcida a nuvem eletrônica do íon negativo. Essa polarização do íon negativo leva a criação de uma densidade de carga extra entre os dois núcleos atômicos, i.e., a covalência parcial. Íons negativos grandes são mais facilmente polarizados, mas, normalmente, o efeito só tem relevância quando íons positivos com cargas de 3+ (ex., Al3+) estão envolvidos (ex., AlCl3 puro é uma molécula covalente). No entanto, íons com carga 2+ (Be2+) ou até com carga 1+ (Li+) demonstram algum grau de polarização devido ao seu pequeno raio atômico (ex., LiI é iônico, mas tem algum caráter covalente). O Grau de Polarização depende da relação de carga e do tamanho do íon, geralmente chamada de densidade de carga.
Estrutura iônica[editar | editar código-fonte]
Compostos iônicos no estado sólido formam uma estrutura iônica contínua em um cristal iônico. A forma mais simples de cristal iônico é um cúbico simples. Nessa forma todos os átomos estão posicionados nas extremidades de um cubo. Essa célula unitária tem a massa que é a mesma de 1 dos átomos envolvidos. Quando todos os íons têm aproximadamente o mesmo tamanho, eles podem formar uma estrutura igual chamada cúbica de face-centrada (onde a massa é 4 vezes massa atômica), mas, quando os íons têm tamanhos diferentes, a estrutura é geralmente cúbica de corpo-centrado (2 vezes a massa). Em retículos iônicos o número de coordenação se refere ao número de íons que cada retículo está ligado.
A estrutura do cristal iônico é dependente das energias de coesão existentes no cristal, que, por sua vez, são as energias de atração e repulsão que existem entre os átomos que fazem parte do cristal iônico. Conforme já descrito, as interações são coulômbicas, ou seja, eletroestáticas e a energia pode ser calculada pela seguinte relação:

Onde k = 4πԑ0, com ԑ0 sendo a constante de permissividade do vácuo, Z+ e Z_ referem-se às cargas dos compostos e r representa a distância entre as cargas. Ainda assim, uma outra fórmula pode relacionar melhor o fenômeno, considerando todas as interações existentes entre todos os átomos e considerar o fator geométrico do sólido, através da constante de Madelung (A, A = 0,69315) e a constante de Born-Landé (B), que relaciona as forças de repulsão existentes quando há a superposição de distribuições eletrônicas, inclusive:

Em que n é o expoente de Born. O segundo membro dessa soma representa a força de repulsão existente no cristal iônico.[3]
Ligações iônicas versus ligações covalentes[editar | editar código-fonte]
Em uma ligação iônica, os átomos estão ligados pela atração de íons com cargas opostas, enquanto que em uma ligação covalente, os átomos estão ligados por compartilhamento de elétrons. Na ligação covalente, a geometria molecular de cada átomo é determinada pelas regras da VSEPR (Valence Shell Electron Pair Repulsion Theory - Teoria da repulsão entre os pares de elétrons da camada de valência), enquanto que, em materiais iônicos, a geometria segue as regras do empacotamento máximo e a resultante das cargas desses íons no empacotamento tende a ser nula.
Há, no entanto, uma tênue linha divisória entre a ligação covalente e a iônica. Com relação à eletronegatividade dos elementos participantes, Linus Pauling estabeleceu que se a diferença de eletronegatividade ( ) for superior a 1,7, a ligação é iônica. No entanto, pode-se dizer que a ligação Carbono-Bromo (
) for superior a 1,7, a ligação é iônica. No entanto, pode-se dizer que a ligação Carbono-Bromo ( < 1,65) tem caráter levemente iônico.
< 1,65) tem caráter levemente iônico.
 ) for superior a 1,7, a ligação é iônica. No entanto, pode-se dizer que a ligação Carbono-Bromo (
) for superior a 1,7, a ligação é iônica. No entanto, pode-se dizer que a ligação Carbono-Bromo ( < 1,65) tem caráter levemente iônico.
< 1,65) tem caráter levemente iônico.De uma maneira mais precisa e mais visualizável, o Triângulo de Ketelaar[4] é uma proposta de entendimento eficaz do caráter iônico, covalente e/ou metálico, do composto a ser analisado. Essa espécie de diagrama leva em consideração a eletronegatividade de Pauling (dado expresso na tabela periódica) e a diferença de eletronegatividade entre os átomos participantes da interação. Com isso, o caráter iônico de certos compostos pode ser observado de maneira mais precisa e, além disso, o caráter covalente dos compostos considerados iônicos pode ser verificado também. Não apenas esses, mas o caráter metálico também pode ser verificado nesse diagrama. Compostos como o HF (fluoreto de hidrogênio) é considerado um composto covalente, porém, quando observado sob a ótica do Triângulo de Ketelaar, demonstra um acentuado caráter iônico. As três características (iônica, metálica e covalente) são representadas em cada um dos vértices do triângulo e, quanto mais houver proximidade dos vértices, maior proximidade do caráter designado por este.
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG]
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG]
.
termodinâmica quântica e relativista Graceli de vibrações e pressões no SDC GRACELI
segunda-feira, 4 de fevereiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Quanto ao conhecimento da força[editar | editar código-fonte]
Vibração determinística[editar | editar código-fonte]
Ocorre quando o valor ou magnitude da excitação, seja ela força ou movimento, aplicada no sistema é conhecida em qualquer instante de tempo.
Vibração aleatória[editar | editar código-fonte]
É aquela que não pode ser prevista, os seus valores não são conhecidos. Como exemplos podemos citar a velocidade do vento e o movimento do solo durante um terremoto.
Quanto aos diversos elementos[editar | editar código-fonte]
- Vibração linear
Ocorre quando todos os componentes básicos do sistema (massa, mola e amortecedor) se comportam de maneira linear, o que não ocorre com a mola depois de uma certa deformação, e portanto passa a possuir um comportamento não linear.
- Vibração não linear
Quando qualquer elemento se comporta de maneira não linear no sistema, temos a vibração não linear, e portanto teremos que lidar com equações diferenciais mais complexas de se resolver e de análises melhor desenvolvidas, cujo principio da superposição não é válido como para o caso de vibrações do tipo linear. Todo sistema tende a comportar-se não linearmente com o aumento da amplitude, como no caso da mola já mencionado.
Forças de excitação[editar | editar código-fonte]
Um sistema mecânico ou estrutural sofre vibração forçada sempre que energia externa é fornecida ao sistema durante a vibração. A energia externa pode ser fornecida ao sistema por meio de uma força aplicada ou por uma excitação de deslocamento imposta. A natureza da força aplicada ou da excitação de deslocamento pode ser da natureza harmônica, não harmônica mas periódica, não periódica ou aleatória. A resposta de um sistema à excitação harmônica é denominada resposta harmônica. A excitação não-periódica pode ser de curta ou longa duração. A resposta de um sistema dinâmico a excitações não-periódicas aplicadas repentinamente é denominada resposta transitória. [1]
Força harmônica[editar | editar código-fonte]
A vibração produzida por uma máquina rotativa desbalanceada, as oscilações de uma chaminé alta provocadas por emissão de vórtices (redemoinhos) sob vento constante e o movimento vertical de um automóvel sobre a superfície senoidal de uma estrada são exemplos de vibração excitada harmonicamente.
 Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou
Considere a resposta dinâmica de um sistema com um grau de liberdade (física) sob excitação harmônica da forma ou  ou
ou  . Onde
. Onde  é a amplitude,
é a amplitude,  é a frequência e
é a frequência e  é o ângulo de fase da excitação harmônica. O valor de
é o ângulo de fase da excitação harmônica. O valor de  depende do valor de
depende do valor de  em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]
em t=0 e normalmente é considerado zero. Sob uma excitação harmônica, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema também será harmônica. Se a frequência de excitação coincidir com a frequência natural do sistema, a resposta do sistema será muito grande. Essa condição conhecida como ressonância , deve ser evitada, para impedir falha do sistema. [1]- Força harmônica pelo desbalanceamento rotativo[1]
Massas desbalanceadas em máquinas rotativas são grandes causadoras de vibração em vários casos de engenharia, como exemplo mais clássico as rodas de um carro que quando estão desbalanceadas causam trepidações no veículo. Um sistema é dito desbalanceado quando o centro de massa desse sistema não coincide com seu centro de rotação. Uma representação simplificada dessa situação pode ser visualizada na figura ao lado. A máquina possui massa  e há uma outra massa
e há uma outra massa  desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez
desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez  e a um amortecedor viscoso de constante de amortecimento
e a um amortecedor viscoso de constante de amortecimento  . Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga
. Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga  . Essa força pode ser decomposta em componentes horizontal
. Essa força pode ser decomposta em componentes horizontal  que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical
que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical  que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular
que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular  . Sendo
. Sendo  a amplitude da vibração,
a amplitude da vibração,  a frequência de oscilação da massa desbalanceada e
a frequência de oscilação da massa desbalanceada e  o ângulo de fase. Os valores de
o ângulo de fase. Os valores de  e
e  são
são
 e há uma outra massa
e há uma outra massa  desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez
desbalanceada a uma distância e do seu centro de rotação que é denominada excentricidade. Esse sistema está acoplado a uma mola de rigidez  e a um amortecedor viscoso de constante de amortecimento
e a um amortecedor viscoso de constante de amortecimento  . Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga
. Podemos relacionar a rotação dessa massa desbalanceada a uma força centrífuga  . Essa força pode ser decomposta em componentes horizontal
. Essa força pode ser decomposta em componentes horizontal  que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical
que será anulada pelo anteparo fixador dessa máquina, como uma parede, e uma componente vertical  que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular
que agirá sob o conjunto mola-amortecedor e o fará vibrar. Para esse fenômeno podemos aproveitar dos resultados de outros fenômenos de vibração e descrever a solução particular  . Sendo
. Sendo  a amplitude da vibração,
a amplitude da vibração,  a frequência de oscilação da massa desbalanceada e
a frequência de oscilação da massa desbalanceada e  o ângulo de fase. Os valores de
o ângulo de fase. Os valores de  e
e  são
são![{\displaystyle X={\frac {me\omega ^{2}}{[(k-M\omega ^{2})^{2}+(c\omega )^{2}]^{1/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78db6ea9fb5792e0e3e47e927459f3ad2b08892e)

Equação de movimento[editar | editar código-fonte]
Se uma força  agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:
agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:  . Visto que essa equação é não-homogênea, sua solução geral
. Visto que essa equação é não-homogênea, sua solução geral  é dada pela soma da solução homogênea
é dada pela soma da solução homogênea  com a solução particular
com a solução particular  . A solução homogênea, que é a solução da equação homogênea
. A solução homogênea, que é a solução da equação homogênea  representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular
representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular  , que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
, que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
 agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:
agir sobre um sistema massa-mola viscosamente amortecido, a equação de movimento pode ser obtida pela segunda lei de Newton:  . Visto que essa equação é não-homogênea, sua solução geral
. Visto que essa equação é não-homogênea, sua solução geral  é dada pela soma da solução homogênea
é dada pela soma da solução homogênea  com a solução particular
com a solução particular  . A solução homogênea, que é a solução da equação homogênea
. A solução homogênea, que é a solução da equação homogênea  representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular
representa a vibração livre do sistema, na qual desaparece com o tempo sob cada uma das condições de amortecimento (subamortecido, amortecido crítico e superamortecido) e sob todas as condições iniciais. Assim, a solução geral da equação obtida pela segunda lei de Newton reduz-se a particular  , que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]
, que representa a vibração em regime permanente. O movimento em regime permanente está presente, contanto que a função forçante esteja presente. [1]Podemos perceber que  desaparece e
desaparece e  torna-se
torna-se  após algum tempo (
após algum tempo ( na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema
na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema  ,
,  e
e  .
.
 desaparece e
desaparece e  torna-se
torna-se  após algum tempo (
após algum tempo ( na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema
na Figura 2). A parte do movimento que desaparece devido ao amortecimento (a parte da vibração livre) é denominada transitória. A taxa à qual o movimento transitório se degrada depende dos valores dos parâmetros do sistema  ,
,  e
e  .
.Força periódica[editar | editar código-fonte]
Excitação que se repete em certo período, porém com intensidades diferentes. Um exemplo prático são motores de combustão interna. Se a força for periódica, mas não-harmônica, ela pode ser substituída por uma soma de funções harmônicas por da expansão da série de Fourier. Usando o princípio da superposição, a resposta do sistema pode ser determinada pela superposição das respostas às funções forçantes harmônicas individuais.[1]
De acordo com a teoria desenvolvida pelo matemático e físico francês Jean Baptiste Joseph Fourier, qualquer função periódica F(t), com período T, pode ser representada por uma série infinita da forma abaixo:

onde  e onde os coeficientes
e onde os coeficientes  ,
,  , e
, e  são dados pelos cálculos a seguir
são dados pelos cálculos a seguir
 e onde os coeficientes
e onde os coeficientes  ,
,  , e
, e  são dados pelos cálculos a seguir
são dados pelos cálculos a seguir


Os coeficientes  ,
,  e
e  , são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
, são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
 ,
,  e
e  , são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
, são chamados de coeficientes de Fourier. Dessa forma, a equação de movimento para sistemas excitados por uma força desse tipo pode ser expressa como
Força transitória[editar | editar código-fonte]
Excitação caracterizada por uma liberação de energia grande em um intervalo curto de tempo. Inúmeros exemplos descrevem este tipo de força: explosão, impacto, etc
Força aleatória[editar | editar código-fonte]
São forças de excitação que não descrevem um padrão determinístico que possa ser definido por uma equação. Para tratar sistemas excitados por forças aleatórias é necessário utilizar métodos estatísticos. Fenômenos aeroelásticos são exemplos de sistemas excitados por forças aleatórias, como forças em asas de aviões, ventos em colunas de pontes, etc.
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
ou
- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD - xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
ou- xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD - xx
= entropia reversível
xdecadimensionalxT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLlD
Pressão (símbolo  ) é a relação entre uma determinada força e sua área de distribuição.
) é a relação entre uma determinada força e sua área de distribuição.
 ) é a relação entre uma determinada força e sua área de distribuição.
) é a relação entre uma determinada força e sua área de distribuição.O termo pressão é utilizado em diversas áreas da ciência como uma grandeza escalar que mensura a ação de uma ou mais forças sobre um determinado espaço, podendo este ser líquido, gasoso ou mesmo sólido. A pressão é uma propriedade intrínseca a qualquer sistema, e pode ser favorável ou desfavorável para o homem: a pressão que um gás ou vapor exerce sobre a pá de uma hélice, por exemplo, pode ser convertida em trabalho. Por outro lado, a pressão da água nas profundezas do oceano é um dos grandes desafios para os pesquisadores que buscam novas fontes de recursos naturais.[1]
Expressões matemáticas[]
Para problemas que envolvem gases e sólidos a expressão matemática utilizada para expressar pressão é dada por:
ou
Onde:
é a pressão;
é a força normal a superfície;
é a área total onde a força é aplicada.
Para líquidos, a pressão pode ser escrita como:
ou
Onde:
é a pressão em um ponto específico ou a diferença entre a pressão inicial e final do sistema;
é a massa específica do líquido. ;
é a aceleração gravitacional;
é a profundidade do ponto dentro do líquido.
Podemos descobrir a pressão de um gás a determinada temperatura e volume através da equação do gás ideal:
Onde:
é a pressão do gás;
é o número de mols do gás;
é a constante dos gases perfeitos;
é o volume do gás.
A pressão é uma grandeza escalar. O vetor força muda conforme a orientação do plano onde é aplicado, porém o valor da pressão permanece o mesmo, ou seja, é independente de direção. O vetor força que caracteriza a pressão pode ser relacionado ao vetor da força normal, uma vez que ambos são perpendiculares à superfície. [1]
Unidades[editar | editar código-fonte]
Sendo a definição de pressão: força por unidade de área, analogamente a unidade será newton por metro quadrado (N/m2). Em homenagem a Blaise Pascal, por suas diversas contribuições relativas à pressão, pressão mecânica e hidrostática, a unidade no Sistema Internacional para medir pressão é o Pascal (Pa).
Em geral, a unidade é encontrada na forma de milhar(kPa), uma vez que as medidas de pressão geralmente apresentam valores altos dessa unidade. A pressão exercida pela atmosfera ao nível do mar, por exemplo, corresponde a aproximadamente 101.325 Pa (pressão normal), e esse valor é normalmente associado a uma unidade chamada atmosfera padrão(atm).
Outras unidades[editar | editar código-fonte]
- Atmosfera é a pressão correspondente a 0,760m (760mm) de Mercúrio, com densidade de 13,5951 g/cm³ a uma aceleração gravitacional de 9,80665 m/s².
- Bária é a unidade de pressão no Sistema CGS de unidades e vale uma dyn/cm².
- Bar é um múltiplo da bária, onde 1 bar = 106 bárias.
- PSI (pound per square inch), libra por polegada quadrada, é a unidade de pressão no sistema inglês/americano, onde 1 psi = 0,07 bar.
- milibar ou hectoPascal é um multiplo do pascal, onde 1 hPa = 100 Pa. Geralmente utilizado na meteorologia.
- mmHG, também chamada de Torricelli, é uma unidade de pressão antiga inventada com o surgimento do barômetro, onde 1 mmHG = 133,332 Pa.
- mH2O é uma unidade relativa a pressão necessária para elevar em um metro o nível de uma coluna de água em um barômetro, sendo 1 mH2O = 9806,65 Pa.
- kgf/cm² representa o peso normal do ar ao nível do mar por cm², sendo 1 kgf/cm² = 98066,52 Pa.
| Nomenclatura | Atmosfera | Pascal | Bária | Bar | milibar ou hectopascal | mmHg | mH2O | kgf/cm² |
|---|---|---|---|---|---|---|---|---|
| Unidade | Atm | Pa | Ba | Bar | mBar / hPa | mmHg | mH2O | kgf/cm² |
| Atmosfera | 1,01325×105 | 1,01325×106 | 1,01325 | 1013,25 | 760,0 | 10,33 | 1,033 | |
| Pascal | 9,869×10-6 | 10 | 10-5 | 0,01 | 7,501×10-3 | 1,020×10-4 | 1,019×10-5 | |
| Bária | 9,869×10-7 | 0,1 | 10-6 | 0,001 | 7,501×10-4 | 1,020×10-5 | 1,020×10-2 | |
| Bar | 0,9869 | 100000 | 1000000 | 1000 | 750,1 | 10,20 | 1,020 | |
| mBar ou hPa | 9,869×10-4 | 100 | 1000 | 0,001 | 0,7501 | 1,020×10-2 | 10,20 | |
| mmHg | 1,316×10-3 | 133,3 | 1333 | 1,333×10-3 | 1,333 | 1,360×10-2 | 13,60 | |
| mH2O | 9,678×10-2 | 9807 | 9,807×104 | 9,807×10-2 | 98,06 | 73,56 | 0,100 | |
| kgf/cm² | 0,968 | 9,810×104 | 9,810×105 | 0,9810 | 981,0 | 735,8 | 10,00 |
Instrumentos de medição[editar | editar código-fonte]
Manômetro[editar | editar código-fonte]
O manômetro é um instrumento utilizado para medir a pressão de um líquido ou de um gás.
A experiência pode ser feita de várias maneiras, inclusive o arranjo dos equipamentos pode variar. A técnica para medir a pressão de um fluido consiste em manter o líquido(geralmente mercúrio, devido a sua alta densidade) dentro de um recipiente com duas extremidades que permitam manejar a pressão na entrada e a sua abertura ou fechamento. Nessas extremidades podemos colocar gases ou outros líquidos, dependendo da experiência em questão. De acordo com a altura da coluna de líquido, pode-se estimar a pressão que ela exerce sobre a pressão de entrada (geralmente é a pressão atmosférica) utilizando a equação que relaciona altura e densidade do líquido à pressão que ele exerce no meio.
Outro tipo de manômetro mais sofisticado consiste em um tubo flexível com uma extremidade ligada a um ponteiro e a outra aberta para a passagem de determinado gás ou líquido. Conforme o recipiente enche, a pressão no tubo deforma a geometria do recipiente, que por sua vez acaba deslocando o ponteiro. Esse tipo de manômetro tem um caráter mais prático, e o outro mais didático.[3]
Piezômetro[editar | editar código-fonte]
O piezômetro é um aparelho utilizado para medir a pressão que a água (ou sua ausência) exerce na composição do solo. O equipamento consiste em um tubo no qual uma extremidade é conectada a um recipiente com algum líquido(geralmente mercúrio, devido a sua alta densidade) e a outra é revestida por algum material poroso, como uma esponja, por exemplo. O tubo é então preenchido com água, e o líquido de medição é separado da água por vácuo ou gás. Quando o solo está seco, a água do tubo é absorvida pela terra e a coluna de líquido de medicação sobe. Quando o solo está muito umido o processo contrário ocorre, enchendo completamente o tubo com água e diminuindo a coluna de líquido.
Com a equação para medir pressão em líquidos podemos calcular a poro-pressão(ou carga piezométrica) do solo. Esse tipo de medida é muito útil, pois permite monitorar a umidade do solo e evitar situações extremas, como deslizamentos devido a erosão do solo.[4]
Barômetro[editar | editar código-fonte]

Barômetro feito com uma coluna de mercúrio.
O barômetro é um equipamento que nos permite calcular algumas grandezas indiretamente através da pressão.
O primeiro barômetro consistia em um tubo com um lado fechado e o outro fixado em algum recipiente, de forma a permitir a passagem de algum fluido desse recipiente para dentro do tubo. Adicionando ao pequeno reservatório algum líquido(geralmente mercúrio, devido a sua alta densidade) para que este sirva como um indicador. Conforme sabemos da hidrostática, um líquido exerce pressão igual para todos os lados. Assim sendo, quando a parte externa do recipiente for submetida a determinada pressão, o líquido vai exercer a mesma pressão na parte interna do tubo. Caso essa pressão externa seja maior que a interna, a coluna do líquida vai subir a fim de nivelar o sistema. Caso contrário, a coluna desce e a parte de cima fica com vácuo.
Partindo da equação que relaciona a diferença de altura do líquido com a sua pressão, e sabendo qual a pressão interna do tubo, podemos calcular quanto vale a pressão externa em qualquer lugar. Através dessa experiência (conhecida como experiência de Torricelli) podemos determinar a altura do local onde estamos com relação ao nível do mar. Sabe-se que uma coluna de mercúrio, por exemplo, mede 76cm ao nível do mar, e que esse valor diminui quando alcançamos altitudes maiores, pois a pressão atmosférica é menor.[3]
Pressão em gases[editar | editar código-fonte]
Segundo a teoria cinética dos gases, um gás é composto por um grande número de moléculas que se movimentam muito rápido e de forma aleatoria, causando frequentes colisões entre as moléculas do gás e com as paredes de qualquer tipo de recipiente. Essas moléculas apresentam um certo momento, dado pelo produto entre a massa e a velocidade da molécula. No instante em que uma molécula colide com uma parede, as moléculas transmitem momento à superfície, e como consequencia produzem uma força perpendicular à essa superfície. A soma de todas essas forças oriundas de colisões em uma determinada superfície, dividida pela área da mesma, resulta na pressão exercida por um gás em um determinado recipiente.[1]
Algumas aplicações da pressão nos gases podem ser observadas na utilização da pressão que o vapor da água exerce sobre determinada superfície quando confinado em um espaço fechado. Esse processo pode ser encontrado em usinas nucleares, onde uma pá gira com a pressão do vapor e converte essa energia em eletricidade. Além disso, observamos a pressão em gases sendo utilizada diariamente no freio do ônibus, por exemplo. O freio de veículos pesados conta com um sistema que usa ar comprimido para cessar o movimento.
Pressão em fluidos[editar | editar código-fonte]
Um corpo no estado líquido é caracterizado por apresentar uma distância entre suas moléculas que permite ao corpo adequar-se ao ambiente em que se encontra. As características da pressão nos líquidos é semelhante a que encontramos nos gases: o líquido exerce pressão para todos os lados de um recipiente e em qualquer corpo que for imerso nele.
Segundo o princípio de Pascal, ao exercermos pressão em um fluido confinado em um recipiente, essa é transmitida integralmente a todos os ponto desse recipiente. Uma experiências que pode ajudar a compreender esse princípio é a dos vasos comunicantes: Ao armazenarmos algum líquido em uma estrutura com colunas de volumes diferentes podemos observar que o líquido preenche todas as colunas a mesma altura, desconsiderando as diferenças de volume. Isso prova que o fluido espalha-se uniformemente, portanto, exerce pressão igual em todas as direções.[1] Essa demonstração foi muito importante para o surgimento dos sistemas hidraulicos, essenciais nos dias de hoje.
A pressão em líquidos tem algumas diferenças da pressão nos gases. Com os gases, quanto maior a altitude menor a pressão, já com os líquidos, quanto maior a profundidade, maior a pressão. Isso é facil de ser evidenciado - basta mergulhar e automaticamente sentimos a pressão aumentando. É instintivo pensar que ao furar uma garrafa de água, a vazão de um furo na sua base será maior do que a de um furo lateral(considerando que ambos tem a mesma área). Essa diferença é devida a maior pressão no fundo da garrafa, devido a altura da coluna de água.[3]
Outra característica marcante da pressão nos líquidos e demais estados da matéria é sua propriedade de alterar os outros elementos do conjunto: temperatura, pressão e volume. Podemos perceber isso ao cozinhar feijão em uma panela de pressão: o vapor da água aumenta a pressão no interior da panela, e isso provoca uma alteração do ponto de ebulição da água, que passa a ferver acima dos 100°C. Isso agiliza o processo de cozimento do grão do feijão, que seria muito mais lento se não fosse o advento da panela de pressão.
Pressão em sólidos[editar | editar código-fonte]
Existe uma área da física que aborda o assunto pressão com restrição aos corpos rígidos. Esse assunto é estudado profundamente devido as sua extrema importância. A tensão mecânica, como é chamada, estuda todos os tipos de pressões e tensões que são encontradas dentro ou sobre um corpo material, sendo elas:
- Tensão de tração;
- Tensão de compressão;
- Tensão de cisalhamento;
- Tensão elástica;
- Tensão plástica;
- Tensão de escoamento.[5]
Diferente da pressão nos fluidos, em corpos rígidos os átomos não têm tanta liberdade e acabam tendo seus movimentos restringidos, ou seja, não exercem pressão ao seu redor. Se pegarmos uma pedra e largarmos em uma superfície, a única pressão que a pedra exerce no sistema é a resultante de sua força peso e da área da sua base, que pressiona a mesa. Portanto, percebemos que a pressão dos sólidos é ocasionada necessariamente por uma força(a própria força peso, por exemplo) que usa o sólido como recurso para ampliar sua força e área. Este conjunto de informações é suficiente para refletir sobre as consequências dessas tensões no ambiente em que vivemos.
Uma aplicação para essas observações são os patins. A patinação sobre o gelo utiliza dos artifícios da pressão para proporcionar menos aderência aos praticantes do esporte. Vamos entender por quê:
O metal utilizado como lâmina na sola do sapato de patinação é muito fino, e sua área é muito pequena frente ao peso do patinador. Como a pressão é inversamente proporcional a área de abrangência da força, quanto menor o metal mais pressão será feita sobre o gelo.
Assim como a água, o gelo sofre algumas mudanças de características. A que estamos interessados no momento revela que o gelo sobre os patins está sobre uma pressão tão intensa que acaba trocando de estado da matéria e vira liquido mesmo a temperaturas abaixo de zero. Graças a isso, os patins utilizam a força peso do patinador para derreter uma fina camada de gelo em baixo da lâmina quando está deslizando, aumentando sua velocidade e lubrificando o caminho.[1]
Alguns fenômenos naturais como os glaciares também tem alguns fatores relacionados a pressão que os cubos de gelo exercem um sobre o outro, fazendo com que o gelo mais em baixo derreta e o gelo que está por cima,fazendo uma trilha de água e escoe os blocos até algum rio ou oceano(ou até que sequem).
efeitos Graceli de piezoeletricidade
A piezoeletricidade tem também efeitos proporcionais sobre magnetismo, condutividade térmica e elétrica, dilatações, interações interna e transformações de estruturas, difrações e refrações, emissões e absorções de partículas e energias, momentum térmico, elétrico, dinãmico, magnético, e outros fenômenos. ondas e saltos quântico, estado quântico de partículas, momentum quântico.
A piezoeletricidade tem também efeitos proporcionais sobre magnetismo, condutividade térmica e elétrica, dilatações, interações interna e transformações de estruturas, difrações e refrações, emissões e absorções de partículas e energias, momentum térmico, elétrico, dinãmico, magnético, e outros fenômenos. ondas e saltos quântico, estado quântico de partículas, momentum quântico.

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.
Mecanismo
O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).
O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.[1]
Cristais[editar | editar código-fonte]
Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.
Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.
Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.
A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.[2]
Descrição matemática[editar | editar código-fonte]
A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:[3]

Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinalaplicada.
Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.
Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:

Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.
A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que  e
e  . Assim, temos
. Assim, temos
 e
e  . Assim, temos
. Assim, temos

onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.
Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.
Num material piezoelétrico também interessam os seguintes coeficientes:
- Coeficiente de acoplamento eletro-mecânico:
 é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.- Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:

Aplicações[editar | editar código-fonte]
O fenômeno piezoelétrico é encontrado em aplicações úteis, como a produção e detecção de som, a geração de tensões elevadas, geração de frequências eletrônicas, microbalanças e concentração ultrafina de conjuntos ópticos. É também a base de uma série de técnicas científicas instrumentais com resolução atômica (microscopia de varredura de sonda), e os usos cotidianos, como atuando como fonte de ignição para isqueiros de faísca elétrica, microfones, e as famosas "pílulas" ou cápsulas de guitarra (embora sejam utilizadas em guitarras acústicas, baixos, violoncelos e outros), que representam uma espécie de microfone. O projeto mais arrojado; porém, refere-se à utilização do materiais piezoelétricos em ruas e estradas, onde a pressão causada pela movimentação dos carros podem ser usados para gerar eletricidade de forma barata.
As transformações que ocorrem em cada material:
- Exemplos de transformações mecânico-elétrica
- Medidor de pressão;
- Microfone;
- Isqueiro elétrico;
- Alarme antifurto;
- Agulha do toca-discos.
- Exemplos de transformações elétrico-mecânicas
- Ultrassom;
- Nebulizadores;
- Aparelhos elétricos contra mosquitos;
- Alto-falantes;
Sensores piezoelétricos[editar | editar código-fonte]
Os sensores piezoelétricos mensuram determinados parâmetros físicos, que estão na forma de tensão mecânica ou variações de cargas elétricas. Estes são utilizados para se medir pressão cardíaca e registrar os batimentos cardíacos, emitir ou recepcionar ultrassons a fim de visualizar órgãos humanos através da conversão da energia proveniente das ondas emitidas pelo funcionamento dos órgãos que faz vibrar uma lâmina de material piezoelétrico. Resumidamente, quando se aplica tensão mecânica, há o aparecimento de um potencial elétrico; quando a tensão aplicada for de natureza elétrica, temos uma deformação física.
O princípio de funcionamento de um sensor piezoelétrico reside no fato de que dada dimensão física, pela ação de uma força, é deformada. Dependendo da concepção de um sensor, "modos" diferentes de polarização sobre o elemento piezoelétrico podem ser usados (eles podem ser comprimidos transversalmente, longitudinalmente, ou pela ação de cisalhamento).
A detecção de variações de pressão sob a forma de ondas sonoras é a aplicação mais comum do sensor. Por exemplo, Microfonepiezoelétricos, onde ondas sonoras batem no material piezoelétrico, criando uma tensão que varia. Captadores piezoelétricos funcionam pelo mesmo princípio em guitarras electro-acústicas.
Sensores piezoelétricos mais acurados são utilizados com som de alta freqüência (acima de 20000 Hz) em transdutores de ultrassom para imagens médicas. Cada transdutor possui uma freqüência de ressonância natural, tal que quanto menor a espessura do cristal que o compõem, maior será a sua frequência de vibração e melhor será o sinal que este gerará ou será capaz de emitir.
Para várias técnicas de detecção, o sensor pode atuar tanto como um sensor ou então como captador, sendo então preferencialmente chamado transdutor (termo preferido para descrever quando o dispositivo funciona com ambas aplicações). A maioria dos dispositivos piezoelétricos têm esta propriedade de reversibilidade, sendo que desta forma, materiais piezoelétricos são indiscriminadamente chamadas transdutores. Transdutores de ultrassom, por exemplo, pode projetam ondas de ultrassom no corpo humano, recebem a reverberação desta onda, com frequência diferente da emitida, convertendo-a em sinal elétrico (tensão).
A carga induzida  num material piezo é proporcional a força
num material piezo é proporcional a força  aplicada.
aplicada.
 num material piezo é proporcional a força
num material piezo é proporcional a força  aplicada.
aplicada.
onde  é uma constante piezoelétrica, com unidade Coulomb por Newton.
é uma constante piezoelétrica, com unidade Coulomb por Newton.
 é uma constante piezoelétrica, com unidade Coulomb por Newton.
é uma constante piezoelétrica, com unidade Coulomb por Newton.Os materiais piezoelétricos possuem resistência muito elevada, mas não infinita. Se uma deflexão for aplicada sobre o material, uma corrente infinitesimal seguirá por um circuito, preservando o sinal elétrico gerado pelo piezoelétrico, sendo que a voltagem gerada pode ser mensurada ou ativar outro sensor piezoelétrico deste circuito. Deve-se ressaltar que o sinal decai exponencialmente pela resistência do material piezo somado a resistência externa do circuito.[4]
Padrão de frequência[editar | editar código-fonte]
Materiais piezoelétricos são empregados em relógios como osciladores. Um cristal de quartzo, que utiliza uma combinação dos efeitos de piezoeletricidade direta e inversa para gerar uma série regular de impulsos elétricos cronometrado, que marcam o tempo. O cristal de quartzo (como qualquer material elástico) tem uma frequência natural definida com precisão (devido a sua forma e tamanho), e este é utilizado para estabilizar a frequência de uma tensão elétrica periódica aplicada ao cristal.
O mesmo princípio é aplicado em todos os transmissores e receptores de rádio, e em computadores onde ele cria um pulso de clock. Ambos costumam usar multiplicadores de frequência para atingir faixas gigahertz.
Sonar[editar | editar código-fonte]
Pelos estudos de Leonardo DaVinci no século XV, temos uma descrição simplista, porém clara, da ação de um sonar:
Qualquer outra descrição difere somente em detalhes.
O estudo da natureza das ondas sonoras na água e o modo como elas se propagam permitiu com que se construíssem sistemas acústicos para observação e mapeamento de solos embaixo d'água. Sensores capazes de identificar a energia de ondas acústicas embaixo d'água são chamados Hidrofone, feitos a partir de materiais piezoelétricos.
Os sonares funcionam pela propagação de ondas acústicas (criadas através de sinais digitais eletrônicos) sendo que ele também recebe a volta o sinal acústico que emitiu. Construído com materiais piezoelétricos, este utiliza da energia das ondas para fazer vibrar (sonar) uma película fina que converte a energia proveniente das ondas reverberadas novamente em pulsos elétricos, mas agora com outras intensidades, que são então decodificados em um computador, tratadas, e gerar imagens de regiões abaixo d'água.
O método acústico na fabricação de sonares, o qual não envolve transformações eletroacústicas, representa o método mais rudimentar (baseado na descrição de DaVinci), sendo que este foi amplamente utilizado durante a Primeira Guerra Mundial. Virtualmente, todos os sistemas de sonares, os quais a energia é restrita a forma acústica são utilizados ainda para localizar um alvo quando este é uma fonte primária de som. Neste caso, capta-se apenas a energia proveniente da propagação destas ondas, para então transformá-las em sinas elétricos (através de materiais piezoelétricos) a serem interpretados.
Sonares eletroacústicos são muito mais utilizados, com uma gama maior de aplicações. Porém, para operar, o sonar eletroacústico deve estar parado, muito próximo do local a ser mapeado. Além disso, para ser interpretado, o som deve estar na faixa audível; quando a energia acústica é convertida em energia elétrica, uma vasta gama de equipamentos deve ser aplicada para criar um sinal com características específicas mais convenientes para que os dados possam ser lidos. Neste momento, transdutores como microfones, alto-falantes e fones-de-ouvido (que são excelentes sistemas quando utilizados com deslocamento de massas de ar) se mostram ineficientes com a energia das camadas de água, uma vez que a impedância acústica específica da água (magnitude da resposta a um estímulo) é 4000 vezes maior do que a do ar.
Os sonares eletroacústico são então sistemas muito sensíveis, e desta forma, também são muito suscetíveis a distúrbios e interferências na recepção do sinal. Este tipo de sonar, portanto, ainda é muito estudado e muitos materiais piezoelétricos são testado para que se consiga a melhor relação entre as dificuldades apresentadas por mares e oceanos e pela tecnologia empregada.
Estadologia Graceli – 4. E princípio entrópico tempo / instabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
 ,
,

 = entropia reversível
= entropia reversível
cV ,
,

 = entropia reversível
= entropia reversível
cV = (12/5) π4 R (T/θD)3,

 = entropia reversível
= entropia reversível
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.


 = entropia reversível
= entropia reversível


 = entropia reversível
= entropia reversível


Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
A Teoria do Calor Específico de Einstein, entropia quântica no SDC GRACELI
quarta-feira, 13 de fevereiro de 2019
 ,
, x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
cV
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
cV = (12/5) π4 R (T/θD)3,
x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
A Teoria do Calor Específico de Einstein. Em 1819 (Annales de Chimie et de Physique 10, p. 395), os franceses, o químico Pierre-Louis Dulong (1785-1838) e o físico Aléxis-Thérèse Petit (1791-1820) mostraram que a dilatação de um corpo não é uma função uniforme da temperatura. Com essa informação, começaram a estudar o calor específico (a volume constante) (cV) dos corpos. Então, usando um método de resfriamento que eles haviam desenvolvido, mediram o cV de vários sólidos [bismuto (Bi), chumbo (Pb), cobalto (Co), cobre (Cu), enxofre (S), estanho (Sn), ferro (Fe), níquel (Ni), ouro (Au), platina (Pt), prata (Ag), telúrio (Te), e zinco (Zn)], tomando como base o da água. Por outro lado, ao tomarem como base o peso atômico do oxigênio (O) e considerando-o como unitário, eles descobriram que o produto do cV de cada sólido considerado pelo seu respectivo peso atômico, é sempre constante e aproximadamente igual a 0,38. Em vista deste resultado enunciaram a hoje famosa Lei de Dulong-Petit (LD-P): - Os átomos de todos os corpos simples têm exatamente a mesma capacidade para o calor. Mais tarde, em 1826, quando o químico sueco Jöns Jakob Berzelius (1779-1848) mostrou que o peso atômico do O valia É interessante destacar que uma primeira evidência da quantização de energiadecorreu do modelo dinâmico dos gases proposto, em 1857 (Annalen der Physik 100, p. 497; Philosophical Magazine 14, p. 108), pelo físico alemão Rudolf Julius Emmanuel Clausius (1822-1888). Com efeito, supondo que todas as moléculas tinham energia proporcional à temperatura, ele afirmou: - A energia de uma molécula era igualmente repartida segundo os seus graus de liberdade internos. Com essa hipótese, mais tarde denominada de Lei da Equipartição da Energia, Clausius demonstrou que a relação entre CP e CV, ou seja: CP/CV = A LD-P teve uma primeira explicação teórica realizada por intermédio do Modelo Eletrônico dos Metais (MEM) e, também, uma primeira ideia sobre o papel dos elétrons na condução térmica e elétrica dos metais foi desenvolvida nas duas últimas décadas do Século 19. Com efeito, em 1888 [Applications of Dynamics to Physics and Chemistry (MacMillan, London)], o físico inglês Sir Joseph John Thomson (1856-1940; PNF, 1906) formulou a hipótese de que a condução elétrica nos metais era semelhante à condução de íons(partículas carregadas positivamente ou negativamente) nos eletrólitos. No entanto, advertiu que enquanto nos eletrodos os portadores de carga eram sais, que se dispersavam na massa inerte do solvente, nos metais a corrente elétrica era composta de uma série de portadores de carga elétrica negativa, causada pelo rearranjo dos constituintes moleculares. Quase dez anos depois, em 1897 (Philosophical Magazine 44, p. 295), Thomson descobriu que tais portadores de carga elétrica negativa (posteriormente denominados de elétrons) eram os raios emitidos pelo catodo de uma ampola de Crookes {construída pelo físico inglês William Crookes (1832-1919), em 1875 [Sir Edmund Taylor Whittaker, A History of the Theories ofAether and Electricity (Thomas Nelson and Sons Ltd., 1951)]}. Um ano depois, em 1898 (Annalen der Physik 66, p. 353; 545; 1199), o físico alemão Carl Victor Eduard Riecke (1845-1915) demonstrou que a condutividade elétrica (σ) poderia ser calculada por intermédio de uma teoria envolvendo elétrons livres. Dois anos depois, em 1900 (Rapportes Présentées auCongrès du Physique 3, p. 138), Thomson formulou pela primeira vez a hipótese de que as eletricidades vítrea (+) e resinosa (-) [propostas pelo físico francês Charles François de Cisternay Du Fay (1698-1739), entre 1733 e 1734 (vide verbete nesta série)] representavam diferentes papéis no processo da condução elétrica. Assim, a carga resinosa (elétrons) poderia se mover livremente entre os átomos do metal. Por outro lado, a carga vítreapermanecia mais ou menos fixa nos átomos metálicos (no Século 20 foram denominadas de prótons). Ainda em 1900, o físico alemão Paul Karl Ludwig Drude (1863-1906) esboçou um primeiro modelo para estudar as propriedades: térmica e elétrica dos metais. Inicialmente (Physikalische Zeitschrift 1, p. 161), considerou o metal como sendo um gás de íons móveis, caracterizados por suas cargas (ei), massas (mi), densidades (Ni), livre-caminhos médios (ℓi) e velocidades médias (vi). Ainda em 1900 (Annalen der Physik 1, p. 566; 3, p. 369), Drudesimplificou seu modelo assumindo que somente os elétrons (de carga e e massa m) eram móveis. O MEM desenvolvido por Thomson, Riecke e Drude foi retomado pelo físico holandês Hendrik Antoon Lorentz (1853-1928; PNF, 1902) em uma série de artigos escritos em 1905 (Proceedings of the Royal Academy of Sciences, Amsterdam 7, p. 438; 585; 684) e 1907 (Jahrbuch der Radioaktivität und Elektronik 4, p. 125). Nesses trabalhos, Lorentz assumiu que os átomos de um metal eram fixos e que os elétrons se deslocavam rapidamente entre seus interstícios. Além do mais, desprezou suas colisões com os átomos fixos considerados por ele como esferas elásticas e fixas. Esse modelo de Lorentz foi generalizado pelo físico dinamarquês Niels Henrik David Bohr (1885-1962; PNF, 1922), Apesar do relativo sucesso do MEM de Drude-Lorentz-Bohr (MEM/D-L-B), principalmente na dedução da Lei de Wiedemann-Franz [essa lei empírica foi anunciada em 1853 (Annalen der Physik und Chemie 89, p. 457), pelos químicos alemães Gustav Heinrich Wiedemann (1826-1899) e Johann Carl Rudolph Franz (1826-1902) ao descobriram que para um intervalo de temperaturas absolutas (T) não muito baixas, a condutividade elétrica (σ) dos metais era aproximadamente proporcional a sua condutividade térmica (κ); tal lei foi confirmada, em 1881, pelo físico dinamarquês Ludwig Valentin Lorenz (1829-1891): A dependência assinalada acima foi demonstrada por Einstein, em 1907 (Annalender Physik 22, p. 180) ao considerar que a energia média (  , , onde β = (hν)/(kBT), h sendo a constante de Planck, e ν é a frequência correspondente à radiação térmica decorrente da temperatura absoluta (T). Ora, sendo cV cV expressão essa que mostra ser cV(T). Note-se que para o caso A dependência teórica de cV com T3 foi encontrada, em 1912 [Archives desSciences Physique et Naturelles (Genève) 33, p. 256; Annales de Physique (Leipzig) 39, p. 789] pelo físico e químico Petrus Joseph Wilhelm Debye (1884-1966; PNQ, 1936) ao propor um modelo no qual um sólido (não-metálico) é considerado como um contínuo elástico, cujos osciladores harmônicos que o constituem vibram em diferentes frequências. Estas decorrem naturalmente desse modelo, já que o movimento dos átomos em um sólido provoca ondas sonoras que viajam para frente e para trás, entre as fronteiras do sólido, resultando ondas estacionárias com modos independentes de vibração, isto é, com várias frequências. Desse modo, considerando a quantização planckiana e a Lei de Distribuição de Maxwell-Boltzman (ver verbetes nesta série), Debye demonstrou que quando T → 0, tem-se: cV = (12/5) π4 R (T/θD)3, onde θD = hν/kB, é a temperatura de Debye. É oportuno destacar que, ainda em 1912 (Physikalische Zeitschrift 13, p. 297), o físico alemão Max Born (1882-1970; PNF, 1954) e o engenheiro húngaro Theodore von Kármán (1881-1963) estudaram o problema do cV dos sólidos considerando ondas progressivas deslocando em uma estrutura reticular (lattice) cristalina, sob condições de periodicidade na fronteira do cristal. Logo depois, em 1913 (Physikalische Zeitschrift 14, p. 15; 65), Born e von Kármán mostraram que o resultado que haviam encontrado no trabalho de 1912 reproduzia os resultados de Einstein (1907) e Debye (1912). Concluindo este verbete, é oportuno registrar que a estrutura espacial de um cristal foi descoberta, em 1912 (Sitzungsberichte der Bayerischen Akademie der Wissenschaften zu München, p. 303), pelos físicos alemães Walther Friedrich (1883-1968), Paul Kniping (1883-1935) e Max Felix Theodor von Laue (1879-1960; PNF, 1914) ao realizarem experiências sobre a difração de raios-X por cristais (vide verbete nesta série). |
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
P
Teoria de Regge no sdc Graceli
sábado, 16 de fevereiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Em física quântica, a Teoria de Regge é o estudo das propriedades analíticas de dispersão como função de momento angular. Por exemplospin electrónico ( elétrons) podem apresentar movimento de rotação em dois sentidos diferentes, por isso é que dois elétrons podem ocupar o mesmo nível ao mesmo tempo, ou 4 ou 8… . Elétrons e Quarks todos possuem Spin de 1/2 e Grávitons Spin 2[1]. Aplicando a matemática Função Beta foi possível explicar a presença dessas linhas retas, como sendo filamentos[2]. Assim nasceu a primeira teoria da corda chamada Primeira-quantificação da corda que se dividiram em cordas abertas e cordas fechadas. Cordas abertas têm menos modos de vibração que cordas fechadas, pois possuem as pontas livres, na corda fechada para manter as pontas fixas é necessário mais modos de vibração[3]. Esta teoria não-relativística foi desenvolvido por Tullio Regge, em 1957.
Pólos de Regge[editar | editar código-fonte]
O exemplo mais simples dos pólos de Regge é fornecido pela abordagem mecânica quântica do potencial de Coulomb  ou, diferentemente, pelo tratamento mecânico quântico da ligação ou dispersão de um elétron de massa e carga elétrica
ou, diferentemente, pelo tratamento mecânico quântico da ligação ou dispersão de um elétron de massa e carga elétrica  de um próton de massa
de um próton de massa  e carga
e carga  . A energia
. A energia  da ligação do elétron ao próton é negativa, enquanto que, para a dispersão, a energia é positiva. A fórmula para a energia de ligação é a expressão:
da ligação do elétron ao próton é negativa, enquanto que, para a dispersão, a energia é positiva. A fórmula para a energia de ligação é a expressão:
 ou, diferentemente, pelo tratamento mecânico quântico da ligação ou dispersão de um elétron de massa e carga elétrica
ou, diferentemente, pelo tratamento mecânico quântico da ligação ou dispersão de um elétron de massa e carga elétrica  de um próton de massa
de um próton de massa  e carga
e carga  . A energia
. A energia  da ligação do elétron ao próton é negativa, enquanto que, para a dispersão, a energia é positiva. A fórmula para a energia de ligação é a expressão:
da ligação do elétron ao próton é negativa, enquanto que, para a dispersão, a energia é positiva. A fórmula para a energia de ligação é a expressão:Considerada como uma função complexa de  , essa expressão descreve no plano-
, essa expressão descreve no plano- complexo um caminho que é chamado de "trajetória de Regge". Assim, nesta consideração, o momento orbital pode assumir valores complexos.
complexo um caminho que é chamado de "trajetória de Regge". Assim, nesta consideração, o momento orbital pode assumir valores complexos.
 , essa expressão descreve no plano-
, essa expressão descreve no plano- complexo um caminho que é chamado de "trajetória de Regge". Assim, nesta consideração, o momento orbital pode assumir valores complexos.
complexo um caminho que é chamado de "trajetória de Regge". Assim, nesta consideração, o momento orbital pode assumir valores complexos.As trajetórias de Regge podem ser obtidas para muitos outros potenciais, em particular também para o potencial de Yukawa[4].
As trajetórias de Regge aparecem como pólos da amplitude de dispersão[5] ou na matriz-S relacionada. No caso do potencial de Coulomb considerado acima, esta matriz-S é dada pela seguinte expressão:
Esta função gama é uma função meromorfa do seu argumento com pólos simples em  . Assim, a expressão para
. Assim, a expressão para  (a função gama no numerador) possui pólos precisamente nesses pontos, que são dadas pela expressão acima para as trajetórias de Regge; por isso o nome pólos de Regge.
(a função gama no numerador) possui pólos precisamente nesses pontos, que são dadas pela expressão acima para as trajetórias de Regge; por isso o nome pólos de Regge.
 . Assim, a expressão para
. Assim, a expressão para  (a função gama no numerador) possui pólos precisamente nesses pontos, que são dadas pela expressão acima para as trajetórias de Regge; por isso o nome pólos de Regge.
(a função gama no numerador) possui pólos precisamente nesses pontos, que são dadas pela expressão acima para as trajetórias de Regge; por isso o nome pólos de Regge.Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Postado por cienti
Estatística quântica no sistema decadimensional e categorial Graceli
quinta-feira, 14 de fevereiro de 2019

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D

x

x
 = entropia reversível
= entropia reversívelx
decadimensional
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Uma estatística quantica, no contexto da mecânica quântica e no da mecânica estatística, é a descrição de como a energia de cada um dos entes unitários constituintes de um ensemble está distribuida, dada uma energia total E constante, sob a restrição de que:
- a energia passa a ser quantizada;
- as partículas objeto de estudo passam a ser indistinguíveis.
Isso é feito expressando-se as probabilidades relativas de uma partícula com energia 

De modo clássico, a probabilidade é dada por:

onde

é a chamada função de partição
Nos casos quanticos, o que muda é a questão da quantização do espaço de fase, o que impõe um "volume" mínimo de célula possível nesse espaço.
Estados de Graceli de matéria, energias, momentuns, inércias, e entropias.
Estados térmico.
Estado quântico.
De dilatação.
De entropia.
De potencia de entropia e relação com dilatação.
De magnetismo [correntes, momentum e condutividades]..
De eletricidade [correntes, momentum e condutividades].
De condutividade.
De mometum e fluxos variados.
De potencial inercial da matéria e energia.
De transformação.
De comportamento de cargas e interações com elétrons.
De emaranhamentos e transemaranhamentos.
De paridades e transparidades.
De radiação.
Radioatividade.
De radioisótopos.
De relação entre radioatividade, radiação, eletromagnetismo e termoentropia.
De capacidade e potencialidade de resistir a pressão, a capacidade de resistir a pressão e transformar em entropia e momentum.
De resistir à temperaturas.
E transformar em dilatação, interações entre partículas, energias e campos.
Estado dos padrões de variações e efeitos variacionais.
Estado de incerteza dos fenômenos e entre as suas interações.
E outros estados de matéria, energia, momentum, tipos de inércia [como de inércia potencial de energias magnética, elétrica, forte e fraca, dinâmica, geométrica [côncava, convexa e plana] em sistema.
E que todos estes tipos de estados tendem a ter ações de uns sobre os outros, formando um aglomerado de fenômenos de efeitos na produção de novas causas. E de efeitos variacionais de uns sobre os outros, ou seja, um sistema integrado.
Sobre padrões de entropia.
Mesmo havendo uma desordem, esta desordem segue alguns parâmetros futuros e que dependem de condições dos estados de Graceli, ou seja, a desordem segue alguns padrões e ordens conforme avança e passa por fases e agentes fenomênicos, estruturais e geométricos.
Porem, a reversibilidade se torna impossível, aumenta a instabilidade e as incertezas de posição, intensidade, variações, efeitos e outros fenômenos conforme as próprias intensidades de dilatações, e agentes e estados envolvidos.
Levando em consideração que mesmo havendo ordem não é possível a reversibilidade do estado e condições em que se encontravam a energia, matéria, momentum, inércias, dimensões, e outros agentes.
A temperatura pode voltar ao seu lugar e ao seu ponto inicial, mas não as estruturas das partículas, as intensidades infinitésimas de padrões de energias, e nem o grau de oscilações que a energias, as interações, as transformações que passam estas partículas e suas energias, estruturas e interações, e as interações e intensidades de grau de variação de cada agente.
Porem, a desordem é temporal, ou seja, com o passar do tempo outras ordens e padrões se afirmarão.
Sendo que também a entropia varia conforme intensidade de instabilidade por tempo. E tempo por intensidade de instabilidade.
Assim, segue efeitos variacionais e de incertezas por instabilidade de energia adicionada, e de tempo.
Ou seja, uma grande instabilidade e desordem em pouco tempo vai levar a uma grande e instável por mais tempo uma entropia.
Do que um grande tempo com pequena intensidade de instabilidade e energia adicionada num sistema ou numa variação térmica.
Ou mesmo numa variação eletromagnética, ou mesmo na condutividade.
Princípio tempo instabilidade de Graceli.
Assim, a desordem acaba por encontrar uma ordem se não acontecer nenhuma instabilidade novamente. Pois, as partículas e energias tendem a se reorganizar novamente conforme o passar do tempo, e esta reorganização segue um efeito progressivo em relação à desordem e tempo. Como os vistos acima.
Ou seja, aquela organização anterior não vai mais acontecer, pois, segue o princípio da irreversibilidade, mas outras organizações se formarão conforme avança o tempo de estabilidade.
Postado por physicists Ancelmo Luiz Graceli às 02:43
as dimensões categorias podem ser divididas em cinco formas diversificadas.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
 = entropia reversível
= entropia reversível
matriz categorial Graceli.
tipos, níveis, potenciais, tempo de ação, especificidades de transições de energias, de fenômenos, de estados de energias, físicos [estruturais], de fenômenos, estados quântico, e outros.
paradox of the system of ten dimensions and categories of Graceli.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
a four-dimensional system can not define all the energies, changes of structures, states and phenomena within a structure, that is why there are ten or more dimensions, I have developed and I work with ten, but nature certainly goes beyond ten, with this we move to a decadimensional and categorial universe.
that is, categories ground the variables of phenomena and their interactions and transformations.
and with this we do not have a relationship with mass, but with structure, therefore, a structure carries with it much more than mass, since also mass is related to forces, inertia, resistances and energies.
but structures are related to transitions of physical states, quantum, energies, phenomena, and others.
as well as transitions of energies, phenomena, categories and dimensions.
paradoxo do sistema de dez dimensões e categorias de Graceli.
um sistema de quatro dimensões não tem como definir todas as energias, mudanças de estruturas, estados e fenômenos dentro de uma estrutura, por isto se tem dez ou mais dimensões, desenvolvi e trabalho com dez, mas a natureza com certeza vai alem das dez, com isto caminhamos para um universo decadimensional e categorial.
ou seja, as categorias fundamentam as variáveis dos fenõmenos e suas interações e transformações.
e com isto não se tem uma relação com massa, mas com estrutura, pois, uma estrutura carrega consigo muito mais do que massa, uma vez também que massa está relacionado com forças, inércia, resistências e energias.
mas estruturas está relacionado com transições de estados físicos, quântico, de energias, de fenômenos, e outros.
como também transições de energias, fenômenos, categorias e dimensões.
 = entropia reversível
= entropia reversívelpostulado categorial e decadimensional Graceli.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
TUDO QUE ESTÁ RELACIONADO COM ENERGIA, ESTRUTURAS, FENÔMENOS E DIMENSÕES ESTÁ INSERIDO NO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.
todo sistema decadimensional e categorial é um sistema transcendente e indeterminado.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
1] Cosmic space.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
2] Cosmic and quantum time.
3] Structures.
4] Energy.
5] Phenomena.
6] Potential.
7] Phase transitions of physical [amorphous and crystalline] states and states of energies and phenomena of Graceli.
8] Types and levels of magnetism [in paramagnetic, diamagnetic, ferromagnetic] and electricity, radioactivity [fissions and fusions], and light [laser, maser, incandescence, fluorescence, phosphorescence, and others.
9] thermal specificity, other energies, and structure phenomena, and phase transitions.
10] action time specificity in physical and quantum processes.
Sistema decadimensional Graceli.
1]Espaço cósmico.
2]Tempo cósmico e quântico.
3]Estruturas.
4]Energias.
5]Fenômenos.
6]Potenciais., e potenciais de campos, de energias, de transições de estruturas e estados físicos, quãntico, e estados de fenômenos e estados de transições, transformações e decaimentos.
7]Transições de fases de estados físicos [amorfos e cristalinos] e estados de energias e fenômenos de Graceli.
8]Tipos e níveis de magnetismo [em paramagnéticos, diamagnético, ferromagnéticos] e eletricidade, radioatividade [fissões e fusões], e luz [laser, maser, incandescências, fluorescências, fosforescências, e outros.
9] especificidade térmica, de outras energias, e fenômenos das estruturas, e transições de fases.
10] especificidade de tempo de ações em processos físicos e quântico.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
D
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
[estruturas: isótopos, partículas, amorfos e cristalinos, paramagnéticos, dia, ferromagnéticos, e estados [físicos, quântico, de energias, de fenômenos, de transições, de interações, transformações e decaimentos, emissões e absorções, eletrostático, condutividade e fluidez]].
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].







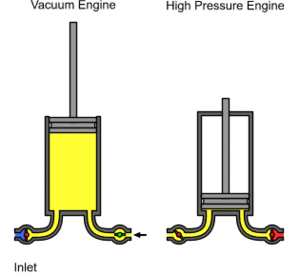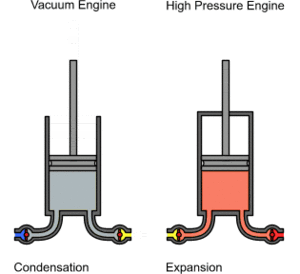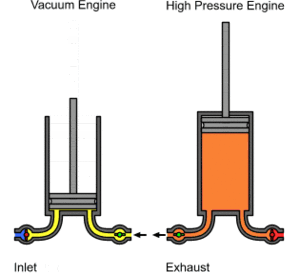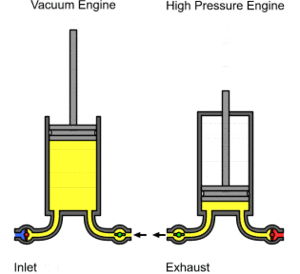




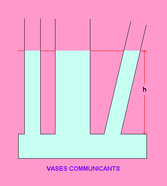



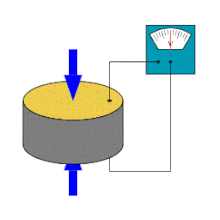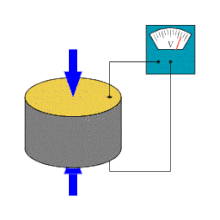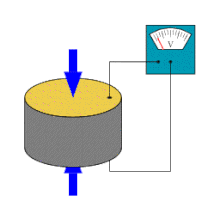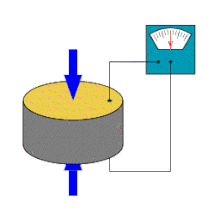

















![{\displaystyle N^{(p=0)}=N\left[1-\left({\frac {T}{T_{0}}}\right)^{d/2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef649cbb75c572cc7590dbf97476d8bab371275f)



